Курсовая работа: Корреляционный анализ финансов предприятия
σ2 yx - среднеквадратическоеотклонениеу оттеоретическихзначенийу х .
Значенияэтихкоэффициентовколеблютсяот 0 до 1. Приη(r)= 0 связьмежупоказателями отсутствует, еслиη (r) = 1, тосвязьфункциональная. Еслиη (r) имеетотрицательноезначение, тосвязьмеждупоказателямиотрицательная.
Привеличинепоказателей:
0,1 - 0,3 . связьслабая;
0,3 - 0,5 . умеренная;
0,5 - 0,7 . заметная;
0,7 - 0,9 . высокая;
0,9 - 0,99 . весьмавысокая.
Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или связана ли продолжительность работы учителя в школе с размером его заработной платы, или с чем больше связан уровень умственного развития учащихся — с их успеваемостью по математике или по литературе и т.п.
Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.
Корреляционные связи — это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. «Оба термина, — пишет Е.В. Сидоренко, — корреляционная связь и корреляционная зависимость — часто используются как синонимы. Зависимость подразумевает влияние, связь — любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.
Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака (Е.В. Сидоренко, 2000).
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Корреляционные связи различаютсяпо форме, направлению и степени (силе).
По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи (см. рис. 1). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности.
По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака - низкие значения другого. При отрицательной корреляции соотношения обратные. При положительной корреляции коэффициент корреляции имеет положительный знак, например r =+0,207 , при отрицательной корреляции - отрицательный знак, например r =—0,207 .
Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.
Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
Максимальное возможное абсолютное значение коэффициента корреляции r =1,00 ; минимальное r =0,00 .
В общем виде формула для подсчета коэффициента корреляции такова:
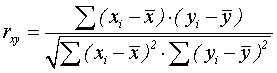
Где:
х i — значения, принимаемые в выборке X,
y i — значения, принимаемые в выборке Y;
![]() — средняя по X,
— средняя по X,
![]() — средняя по Y.
— средняя по Y.
Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально.
В формуле подсчета коэффициента корреляции встречается величина ![]() при делении на n (число значений переменной X или Y) она называется ковариацией. Формула предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.
при делении на n (число значений переменной X или Y) она называется ковариацией. Формула предполагает также, что при расчете коэффициентов корреляции число значений переменной Х равно числу значений переменной Y.
Прирасчетепарнойкорреляциивначалепроизводитсяотборнаиболееважных (существенных) факторов, влияющихнарезультативныйпоказатель. Этифакторыпомещаютсявтаблицу, вкоторойфакторныепризнакиранжируютсявпорядкевозрастанияилиубывания. Далееданныеизтаблицынаносятсянаплоскостькоординат . строитсякорреляционноеполе. Поформеполяилипутемвизуальногоанализаранжированногорядапроизводитсяобоснованиеформысвязи. Принелинейнойсвязивначалеопределяетсятеоретическоезначениефункцииу х, длячегорешаетсяуравнениерегрессии, описывающеесвязьмеждуизучаемымипоказателями. Затемрассчитываетсякорреляционноеотношение.