где – комплексное число, – коэффициент подобия.

Если , то треугольники и равны. Тогда соотношение (3.1) – признак равенства одинаково ориентированных треугольников, а соотношение (3.2) – признак равенства противоположно ориентированных треугольников.

3.2. Критерий правильного треугольника .

Треугольник ориентирован положительно:

(3.4)

Треугольник ориентирован отрицательно:

(3.5)

3.3 Правильные многоугольники.

где k принимает значения . Все n значений имеют один и тот же модуль

Корням уравнения

соответствуют вершины .

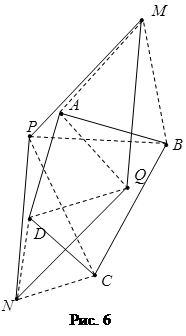З а д а ч а 3. Точки симметричны точке Р ,лежащей в плоскости треугольника ABC , относительно, соответственно, прямых AB , BC , CA . Точки – середины отрезков Докажите, что треугольники и подобны и противоположно ориентированы (рис. 5).

З а д а ч а 4. На сторонах и выпуклого четырёхугольника вне его построены правильные треугольники и а на сторонах и построены правильные треугольники и лежащие с четырёхугольником в одной полуплоскости относительно прямых и соответственно. Докажите, что –параллелограмм (рис. 6).

З а д а ч а 5. Точка делит сторону правильного треугольника в отношении 3:2 считая от точки . Точка делит сторону в отношении 3:14, считая от точки . Отрезки и пересекаются в точке. Докажите, что прямые и перпендикулярны.

З а д а ч а 6. Через центр правильного треугольника проведена прямая. Доказать, что сумма квадратов расстояний от вершин треугольника до прямой не зависит от выбора прямой.

З а д а ч а 7. Пусть d – диаметр окружности, и

– стороны вписанного в неё и описанного около

неё правильных n-угольников. Докажите, что

(рис. 9).

§ 4 Прямая и окружность

4.1. Уравнение прямой .

(4.1)

Пусть коэффициенты a иb не обращаются в нуль одновременно. Приходим к уравнению: которое а) имеет единственное решение при б) имеет бесконечное множество решений при

Отсюда и на основании предыдущих исследований получаем, что уравнение (4.1) определяет а) единственную точку при б) прямую при в) пустое множество при

4.3. Общее уравнение окружности в сопряжённых комлексных координатах . Окружность с центром S ( s ) и радиусом R имеет уравнение

(4.2)