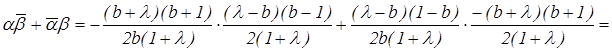Курсовая работа: Метод комплексных чисел в планиметрии
![]() (4.4)
(4.4)
Сравнивая уравнение (4.3) с уравнением (4.2) приходим к выводу, что уравнения (4.3) и (4.2) задают окружность тогда и только тогда, когда ![]() и ab - c – действительное число. Отсюда
и ab - c – действительное число. Отсюда ![]() , а значит, с должно быть действительным числом. Итак, уравнение
, а значит, с должно быть действительным числом. Итак, уравнение
![]() (4.5)
(4.5)
есть уравнение окружности с центром ![]() и радиусом
и радиусом ![]()
4.4. Уравнение окружности по трём данным точкам . Пусть окружность ![]() проходит через точки A , B , C . Тогда однородная линейная система
проходит через точки A , B , C . Тогда однородная линейная система

относительно ![]() имеет ненулевое решение (так как окружности определяются тремя неколлинеарными точками), поэтому её определитель равен нулю:
имеет ненулевое решение (так как окружности определяются тремя неколлинеарными точками), поэтому её определитель равен нулю:
 (4.6)
(4.6)
Это уравнение представляет собой уравнение окружности по трём данным точкам.
4.5. Ортогональные окружности. Две пересекающиеся окружности называются ортогональными , если касательные к ним в их общей точке перпендикулярны. Очевидно, что касательная к одной из окружностей в их общей точке содержит центр другой окружности.
Даны две окружности ( A , R ) и ( B , r ), заданные соответственно уравнениями: ![]() где
где ![]() и
и ![]() где
где ![]() Для того, чтобы эти окружности были ортогональны, необходимо и достаточно, чтобы
Для того, чтобы эти окружности были ортогональны, необходимо и достаточно, чтобы ![]() или
или
![]() (4.7)
(4.7)
или
![]() (4.8)
(4.8)
 З а д а ч а 7. В плоскости даны два отрезка AB иCD . Найдите множество точек М , для каждой из которых площади треугольников MAB иMDC равны (рис. 10).
З а д а ч а 7. В плоскости даны два отрезка AB иCD . Найдите множество точек М , для каждой из которых площади треугольников MAB иMDC равны (рис. 10).
З а д а ч а 9.На гипотенузе AB прямоугольного треугольникаABC дана произвольная точкаP . Докажите, что окружности, описанные около треугольниковAPC и BPC , ортогональны.
 Д о к а з а т е л ь с т в о. Примем вершину С данного треугольника за начальную точку. Пусть точкам А, В, P соответствуют комплексные числа 1, b , p , а центрам окружностей РАС и РВС числа
Д о к а з а т е л ь с т в о. Примем вершину С данного треугольника за начальную точку. Пусть точкам А, В, P соответствуют комплексные числа 1, b , p , а центрам окружностей РАС и РВС числа ![]() (рис. 11). По условию
(рис. 11). По условию ![]() или
или ![]() . Переходя к комплексным числам, получаем:
. Переходя к комплексным числам, получаем: ![]() откуда
откуда ![]() .
.
Руководствуясь (4.6), составим уравнение окружности РВС :
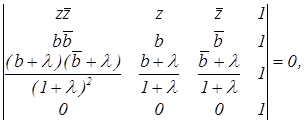
или
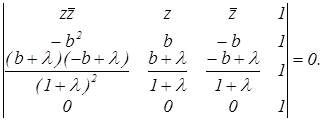
После раскрытия определителя получаем:
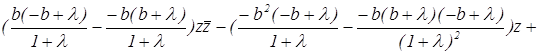
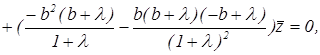
или
![]()
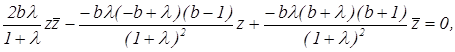
откуда
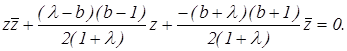
Из уравнения находим: 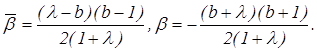
Аналогично, для окружности Р A С имеем:
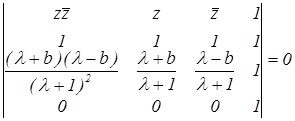
и
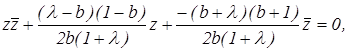
отсюда 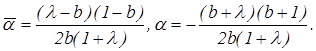
Согласно критерию (4.8) для того, чтобы окружности РАС и РВС были ортогональны необходимо и достаточно, чтобы ![]() Учитывая предыдущие результаты, проверим выполнимость данного критерия:
Учитывая предыдущие результаты, проверим выполнимость данного критерия: