Поэтому, разбивая в процессе ветвления подмножество G’ G на непересекающиеся подмножества G's, G' = , будем предполагать, что φ(G1’) ≥ φ (G’), причем хотя бы для некоторых номеров i0 выполняется строгое неравенство φ() ≥ φ (G’).

4. Вычисление планов (допустимых решений). Если на шаге ветвления с номером k известен план хk, на шаге с номером (k + 1) — план хk+1 и если f(xk+1) < f(xk), то план хkзабывается и вместо него сохраняется план хk+1. Наилучшее из полученных допустимых решений принято называть рекордом.

5. Признак оптимальности. Пусть G = . Тогда план является оптимальным, т.е. , если выполняется условие

f() = φ(Gv) ≤ φ(Gi), i=1, 2, . . . . , s.

6. Оценка точности приближенных решений. Пусть G= ,

φ0 = φ(Gj), xk— рекорд; тогда имеет место следующее неравенство:

φ0 ≤ f(x0) ≤ f(xk).

Разность ∆ = f(xk) - φ0 является оценкой гарантированного отклонения рекорда хk от оптимума х0. Из приведенного неравенства следует, что для ветвления необходимо выбрать множество с минимальным значением нижней оценки.

7. Правило отсева. Пусть снова G = , x0 — оптимум, хk — рекорд. Если φ(Gr) > f(xk), то множество Gr можно отсеять, т.е. исключить из дальнейшего рассмотрения, так как оно не может содержать оптимальных решений. Действительно, пусть x є G; тогда в силу определения оценки f(x) ≥ φ(G') имеем f(x) ≥ φ(Gr) > f(xk) ≥ f(x0).

Правило φ(Gr) > f(xk) гарантирует, что в процессе работы алгоритма ни одно из подмножеств Gr, в которых содержится точное решение x0, не будет отсеяно. Более сильное правило φ(Gr) ≥ f(xk) гарантирует, что хотя бы одно оптимальное решение будет найдено, оно и применяется при практическом решении задач.

8. Конечность алгоритма. Конечность алгоритма следует из конечности множества G.

Под методом ветвей и границ понимается алгоритм решения задачи, имеющий древовидную структуру поиска оптимального решения и использующий результаты решения оценочных задач. Древовидная структура называется обычно деревом ветвления.

Эффективность алгоритма ветвей и границ определяется числом решенных задач. Решение задачи состоит из двух основных этапов. На первом этапе находится оптимальное решение (или близкое к нему). На втором этапе производится доказательство оптимальности полученного решения. Второй этап, как правило, оказывается более трудоемким, чем первый. Это означает, что число подзадач, решаемых до получения оптимума, может оказаться существенно меньше числа подзадач, решаемых для доказательства оптимальности.

2. Постановка задачи коммивояжера

Классическая задача коммивояжера (ЗК) формулируется следующим образом: имеется полный взвешенный ориентированный граф без петель G с множеством вершин N = {1, 2,…, n}; веса всех дуг неотрицательны; в этом графе требуется найти гамильтонов цикл минимального веса.

Исходную информацию по ЗК считаем представленной в виде матрицы размера nxn. S = {sij}, где sij – вес дуги (i, j) графа G, i = , j = , i ≠ j; все элементы главной диагонали матрицы S являются нулями.

В типовой интерпретации вершины 1, 2,…, n графа G – это города. Дуги отображают возможные элементарные переходы. Коммивояжеру, изначально находящемуся в городе 1, необходимо обойти все остальные города, побывав в каждом из них ровно по одному разу, и затем вернуться в город 1. Веса дуг графа трактуются как длины соответствующих элементарных переходов. Требуется найти имеющий минимальную длину допустимый (т.е. удовлетворяющий наложенным требованиям) маршрут коммивояжера. С учетом других возможных интерпретаций, на матрицу S требование симметричности не налагается, не считается обязательным и выполнение неравенства треугольника.

3. Задача коммивояжера методом динамического

программирования

Под методом ветвей и границ понимается алгоритм решения задачи, имеющий древовидную структуру поиска оптимального решения и использующий результаты решения оценочных задач. Древовидная структура называется обычно деревом ветвления.

Один из основных алгоритмов решения ЗК основан на принципе динамического программирования. При изложении этого алгоритма будем придерживаться терминологии, соответствующей приведенной типовой интерпретации задачи.

Пусть i – произвольный город (iÎN), а V – любое подмножество городов, не содержащее города 1 и города i. Через М(i, V ) обозначим совокупность путей, каждый из которых начинается в городе i, завершается в городе 1 и проходит в качестве промежуточных только через города множества V, заходя в каждый из них ровно по одному разу. Через В(i, V ) обозначим длину кратчайшего пути множества М(i, V ). Для решаемой задачи В(i, V) – функция Беллмана. Как очевидно, В(1, {2, 3, …, n}) – искомая минимальная длина простого (без самопересечений) замкнутого пути, проходящего через все города.

Если V – одноэлементное множество, V ={j}, где j ≠ 1 и j ≠ i, то совокупность М (i, V) состоит из единственного пути µ = (i, j, 1). Поэтому

iÎN, jÎ {2, 3,…, n}, j ≠ i.(1.1)

Предположим, что значения функции В(i, V ) для всех iÎN \ {1} и всех возможных k-элементных (k < n – 1) множеств V уже вычислены. Тогда значение В(i, V'), где V' – произвольное (k + 1)-элементное подмножество совокупности N \ {1, i}, вычисляется по формуле

(1.2)

Уравнения (1.1)–(1.12) – рекуррентные соотношения динамического программирования для решения задачи коммивояжера, они обеспечивают реализацию обратного метода Беллмана. Вычислительная сложность задачи равна ,где С – произвольная константа (С > 0), n – число городов.

Пример 1.1 Решить задачу коммивояжера, определяемую матрицей:

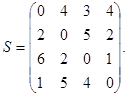
Сначала, пользуясь формулой (1.1), определяем значения В(i, {j}):

В(2, {3}) = 5 + 6 = 11; В(3, {2}) = 2 + 2 = 4; В(4, {2}) = 5 + 2 = 7;

В(2, {4}) = 2 + 1 = 3; В(3, {4}) = 1 + 1 = 2; В(4, {3}) = 4 + 6 = 10.