В(2, {3, 4}) = min [s23 + B(3,{4}); s24 + B(4,{3})] = min(5 + 2; 2 + 10)=7;

В(3, {2, 4}) = min [s32 +B(2,{ 4}); s34 + B(4,{ 2})] = min(2 + 3; 1 + 7 )=5;

В(4, {2, 3}) = min [s42 + B(2,{ 3}); s43 + B(3,{ 2})] = min(5 + 11; 4 +4)=8;

В(1, {2, 3, 4}) = min [s12 + B(2,{3,4}) s13 + B(3,{ 2,4}) s14 + B(4,{2,3 })] =

= min (4 +7; 3 +5; 4 + 8 ) = 8.

Итак, оптимальное значение критерия в рассматриваемом примере равно 8.

Выполненные выделения позволяют определить оптимальный маршрут. Он следующий:

1 ® 3 ® 2 ® 4 ® 1.

Для записи соотношений, по которым реализуется прямой метод Беллмана, введем новые обозначения. Пусть М'(V, i) – совокупность путей, каждый из которых начинается в городе 1, проходит в качестве промежуточных только через города подмножества V, заходя в каждый из них ровно по одному разу, и завершается в городе i; здесь, как и ранее, i – произвольный город (iÎN), а V – любое подмножество N, не содержащее городов 1 и i. Длину кратчайшего пути множества М'(V, i) обозначим В*(V, i). Как очевидно, В*({2, 3, …, n}, 1) – искомая минимальная длина простого (без самопересечений) замкнутого пути, проходящего через все города. Если V – одноэлементное множество, V = {j}, где j ≠ 1 и j ≠ i , то совокупность М'(V, i) состоит из единственного пути µ = (1, j, i). Поэтому

(1.3)

Предположим, что значения функции В*(V, i) для всех iÎN и всех возможных k-элементных (k < n – 1) множеств V уже вычислены. Тогда значение В*(V', i), где V' – произвольное (k + 1)- элементное подмножество совокупности N \{1, i}, вычисляется по формуле

(1.4)

Уравнения (1.3)–(1.4) – рекуррентные соотношения динамического программирования для решения классической задачи коммивояжера, они обеспечивают реализацию прямого метода Беллмана.

Пример 1.2 Методом прямого счета решить задачу коммивояжера, определяемую матрицей:

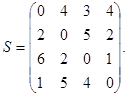
(заметим, что матрица S в данном примере та же, что и в предыдущем).

Сначала, пользуясь формулой (1.3), определяем значения В*( {j }, i):

В*({2}, 3) = 4 + 5 = 9; В*({3}, 2) = 3 + 2 = 5; В*({4}, 2) = 4 + 5 = 9;

В*({2}, 4) = 4 + 2 = 6; В*({3}, 4) = 3 + 1 = 4; В*({4}, 3) = 4 + 4 = 8.

Далее по формуле (1.4) последовательно получаем (в левой части каждого из ниже записанных равенств выделены те значения параметра j, на которых при подсчете реализуется указанный в правой части (1.4) минимум):

В*({2, 3}, 4) = min [B*({2}, 3) + s34; B*({3}, 2) + s24] = min(9 + 1; 5 + 2)= 7;

В*({2, 4}, 3) = min [B*({2}, 4) + s43; B*({4}, 2) + s23] = min(6 + 4; 9 + 5 )= 10;

В*({3, 4}, 2}) = min [B*({3}, 4) + s42; B*({4}, 3) + s32] = min(4 + 5; 8 + 2)= 9;

В*({2, 3, 4}, 1) = min [B*({2, 3}, 4) + s41; B*({2, 4}, 3) + s31; B*({3, 4}, 2) + s21;] = min (7 + 1; 10 +6; 9 + 2 ) = 8.

Итак, оптимальное значение критерия в рассматриваемом примере равно 8.

Выполненные выделения позволяют определить оптимальный маршрут. Он следующий:

1 ® 3 ® 2 ® 4 ® 1.

4. Задача коммивояжера методом ветвей и границ

Другим алгоритмом решения задачи коммивояжера является метод ветвей и границ. В сущности, это некоторая модификация полного перебора решений, оптимизируемая за счет того, что по определенным признакам отсекаются неоптимальные множества перебора.

Формально строится дерево вариантов, начиная от корня. В корне необходимо дать верхнюю и нижнюю оценки. Далее ветвимся. Чем меньший фрагмент дерева придется построить, тем успешнее сработал метод ветвей и границ.