Курсовая работа: Моделирование прогнозирования потребностей как средства повышения эффективности работы транспортных сетей
Более сложным и потому реже используемым методом прогнозирования является факторный анализ. Этот метод состоит в комбинировании большого числа входных переменных в существенно меньшее число групп, включающих сильно коррелирующие переменные. Иногда данный метод используется перед применением регрессионного анализа, благодаря чему последний становится более эффективным.
При прогнозировании потребностей в перевозках людей и грузов возможно также применение имитационных моделей, реализованных на ЭВМ. Обсуждение некоторых наиболее значительных имитационных моделей будет дано при рассмотрении одного из следующих этапов общей схемы исследования. Основное назначение данной модели состоит в предсказании требований к оборудованию летательных аппаратов (прогноз выполняется на срок до 10 лет путем обработки данных о функционировании авиалиний США за предыдущий десятилетний период). Хотя первоначально эта модель предназначалась для предсказания конъюнктуры рынка, тем не менее оказалось возможным прогнозировать тенденции изменения характеристик воздушного транспорта (например, необходимость в новых системах авиалиний, рост объемов перевозок и их стоимости, развитие средств обслуживания пассажиров, улучшение перевозки багажа и грузов, технического обслуживания самолетов, а также общей стоимости системы воздушных сообщений). Метод имитационного моделирования оказался наиболее подходящим для решения задачи, поставленной фирмой Lockheedи имевшей целью формирование требований к развитию большого числа различных авиалиний США.
Для руководителей какой-то определенной авиакомпании вполне естественным является желание предсказать те требования, которым должна отвечать эта авиакомпания, чтобы в будущем выстоять в конкурентной борьбе (возможно, при таком анализе некоторые конкуренты будут выделены особо). С помощью упомянутой модели можно решить эту задачу практически для любой авиакомпании США. Решение осуществляется путем сведения некоторого числа частных требований, составленных сточки зрения отдельной авиакомпании в общую систему требований с последующей конкретизацией оценок, полученных в такой укрупненной модели. Другими словами, данный подход позволяет получать детальный обзор взаимосвязанных характеристик отдельных авиакомпаний. Подобные возможности рассматриваемой модели являются уникальными, и, видимо, имеет смысл попытаться разобрать аналогичные модели и для других видов транспорта, таких, как грузовой автомобильный, железнодорожный и морской транспорт.
Рассмотрим теперь более подробно методы прогнозирования применительно к городскому транспорту. Используемые в данном случае так называемые модели распределения поездок включают в себя модели развития, конфликтующих возможностей, равных возможностей, предпочтений и притяжения. Эти модели построены на различных теоретических предположениях относительно того, каким образом локализация пунктов отправления и назначения, объем перевозок и другие элементы транспортной системы взаимосвязаны с остальными выходными переменными. В качестве последних выступают такие параметры, как планируемый рост тарифов, коэффициенты реальной занятости, расположение торговых зон или зон развлечений и отдыха, пространственное и временное разделение различных городских территорий, факторы привлекательности тех или иных районов города.
Локализация пунктов отправления и назначения может быть определена после разбиения всей городской территории на зоны. Объем перевозок обычно выражается числом поездок, приходящихся либо на одного человека, либо на одно транспортное средство. Общепринятой классификацией поездок в зависимости от пункта назначения является следующая: поездки домой, на работу, в школу, в места отдыха, развлечений, проведения общественных мероприятий, а также регулярные и нерегулярные поездки, связанные с покупкой товаров.
Модели развития позволяют определить будущее распределение поездок между различными парами выделенных зон на основе исходных данных о количестве выездов и въездов для отдельных зон и количестве поездок между различными парами зон. Прогнозируемые значения выходных переменных получаются из известных (на момент составления прогноза) значений с помощью коэффициента развития, который представляет собой оценку ожидаемых изменений в плотности населения и в степени использования территорий рассматриваемых зон. На основе модели развития разработано несколько методов анализа городского транспорта, среди них – методы постоянного коэффициента развития, среднего коэффициента развития, здравого смысла и так называемый детройтский метод. Однако наиболее тщательно разработанным и поэтому широко распространенным является метод Фратера.
Основное предположение, используемое в методе Фратера, состоит в том, что количество поездок из i -той зоны в j -ю для некоторого будущего момента времени пропорционально исходному числу всех выездок из i -той зоны, умноженному на коэффициент развития j -той зоны. Общее соотношение, используемое в методе Фратера, имеет следующий вид:
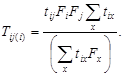
![]()
В этом и следующем выражениях приняты такие обозначения: ![]() - прогнозируемое количество поездок между i -той и j -той зонами, обуславливаемое развитием i -той зоны;
- прогнозируемое количество поездок между i -той и j -той зонами, обуславливаемое развитием i -той зоны; ![]() - прогнозируемое количество поездок между i -той и j -той зонами, обуславливаемое развитием j -той зоны (величину
- прогнозируемое количество поездок между i -той и j -той зонами, обуславливаемое развитием j -той зоны (величину ![]() можно получить из формулы для
можно получить из формулы для ![]() , если в правой части этой формулы индексы i и j поменять местами);
, если в правой части этой формулы индексы i и j поменять местами); ![]() - исходное число всех поездок между i -той и j -той зонами;
- исходное число всех поездок между i -той и j -той зонами; ![]() - коэффициент развития для зоны с номером х , где х принимает множество значений, соответствующих всем рассматриваемым зонам.
- коэффициент развития для зоны с номером х , где х принимает множество значений, соответствующих всем рассматриваемым зонам.
Если через ![]() обозначить прогнозируемое количество всех поездок между i- той и j- той зонами, то имеем
обозначить прогнозируемое количество всех поездок между i- той и j- той зонами, то имеем
 .
.
Поскольку величины, определяемые из двух приведенных выше соотношений, как правило, не удовлетворяют условию
 ,
,
то для его выполнения необходимо использовать метод исследовательных приближений. Модель основана на предположении о том, что число людей, выезжающих из некоторого пункта, прямо пропорционально числу «возможностей», имеющихся на маршруте, и обратно пропорционально числу «реализованных возможностей». В качестве упомянутых «возможностей» можно рассматривать, например, места, в которых может быть предложена работа (для таких людей, ищущих работу), городские и загородные парки (для людей, совершающих поездку с целью отдыха или развлечений), наконец, торговые центры (для людей, выезжающих за покупками).
Модель конфликтующих возможностей математически может быть представлена с помощью выражения
![]() ,
,
где ![]() - количество поездок из i- той зоны в j- тую;
- количество поездок из i- той зоны в j- тую; ![]() - общее количество поездок, начинающихся в i- той зоне; D– количество имеющихся (или отсутствующих) целей на маршрутах ведущих в j- тую зону;
- общее количество поездок, начинающихся в i- той зоне; D– количество имеющихся (или отсутствующих) целей на маршрутах ведущих в j- тую зону; ![]() - количество поездок, заканчивающихся в j- той зоне; L– некоторая оценка вероятности того, что в случайно выбранном пункте назначения может быть достигнута цель отдельной поездки (Lпредставляет собой величину, которую необходимо определить на основе исходных данных; она характеризует степень убывания величины
- количество поездок, заканчивающихся в j- той зоне; L– некоторая оценка вероятности того, что в случайно выбранном пункте назначения может быть достигнута цель отдельной поездки (Lпредставляет собой величину, которую необходимо определить на основе исходных данных; она характеризует степень убывания величины ![]() с увеличением числа целей и длины маршрута), е – основание натурального логарифма.
с увеличением числа целей и длины маршрута), е – основание натурального логарифма.
Основой модели равных возможностей является распределение поездок, характеризуемых одинаковыми временем, расстоянием и стоимостью, по группам однотипных поездок, т.е. поездок с одинаковыми целями. Выделенные таким способом поездки равновероятны в пределах каждой группы.
Модель предпочтения представляет собой модель распределения поездок несколько иного типа, чем рассмотренные выше. Основное предположение, используемое при построении этой модели, состоит в том, что для каждого пункта отправления можно оценить предпочтительность всех возможных пунктов назначения, а для каждого пункта назначения можно оценить предпочтительность всех возможных пунктов отправления. В данной модели сочетание двух определенных пунктов отправления и назначения может быть оптимальным только для одного из пунктов, причем такое сочетание должно удовлетворять некоторым условиям устойчивости.
В модели притяжения, являющейся наиболее широко распространенной моделью распределения поездок, делается оценка количества поездок из i- той зоны в зонуj- ю на основе предположения о том, что рассматриваемая величина прямо пропорциональна некоторому коэффициенту «привлекательности» j- той зоны и обратно пропорциональна, характеризирующему удаленность i- той и j- той зон друг от друга ( в единицах времени или расстояния).
Модель притяжения можно представить математически с помощью следующего выражения:
 ,
,
где ![]() - количество поездок из i -ой зоны, совершаемых благодаря «привлекательности» j- той зоны;
- количество поездок из i -ой зоны, совершаемых благодаря «привлекательности» j- той зоны; ![]() - общее количество поездок, начинающихся в i- той зоне;
- общее количество поездок, начинающихся в i- той зоне; ![]() - общее количество поездок, «привлеченных» j- той зоной;
- общее количество поездок, «привлеченных» j- той зоной; ![]() - эмпирически определяемый коэффициент удаленности (
- эмпирически определяемый коэффициент удаленности (![]() представляется в виде
представляется в виде ![]() или, точнее,
или, точнее, ![]()
, где dij— расстояние между i-й и j-й зонами, abt j— некоторый показатель степени, зависящий от величины d{ jи обычно определяемый с помощью линейной регрессии); Kij— коэффициент, с помощью которого учитываются эффекты социального и экономического характера (величина К13 определяется по исходным данным о распределении поездок). Таким образом, в модели притяжения должны быть предварительно определены (по исходным данным) два параметра —F и К.
Успех этой модели объясняется, главным образом, ее просто той, а также тем, что на агрегированном уровне рассмотрения имеется небольшое число параметров, которые необходимо определять предварительно с требуемой для прогноза степенью точности. Однако вопрос о возможности использования модели притяжения при более низком уровне агрегации вызвал ожив ленную дискуссию.
Модели притяжения, конфликтующих и равных возможностей, а также метод Фратера были подвергнуты сравнительному анализу путем их одновременного использования для изучения распределения поездок в г. Вашингтоне в 1948 и 1955 гг. Оказалось, что прогноз на основе модели притяжения является не сколько более точным и полным, чем на основе модели конфликтующих возможностей. Однако исключение из первой модели коэффициента![]() , учитывающего социально-экономические факторы, может привести к обратному результату. Это обстоятельство указывает, в частности, на то, что степень точности предварительного определения параметра
, учитывающего социально-экономические факторы, может привести к обратному результату. Это обстоятельство указывает, в частности, на то, что степень точности предварительного определения параметра ![]() влияет на точность прогноза, составленного с использованием этой модели. С точки зрения надежности и полезности модели притяжения и конфликтующих возможностей оказались примерно равноценными, хотя для последней, по-видимому, несколько проще проводить предварительное определение соответствующих параметров. В отличие от этих моделей эффективность метода Фратера проявилась лишь при анализе стабильных ситуаций. Если же за период прогноза происходили какие-либо изменения, например в характере использования городской территории, то метод Фратера оказывался совершенно непригодным. Что касается модели равных возможностей, то она по-настоящему не смогла конкурировать с тремя другими моделями, поскольку в рамках рассмотренной зональной структуры г. Вашингтона для нее невозможно было провести определение соответствующих параметров. Кроме того, значительное число небольших зон крайне затруднило установление оптимальных тарифов на проезд, что является серьезным недостатком модели равных возможностей, так как во многих исследованиях, связанных с использованием городской территории, необходимо рассматривать как раз весьма детальное разбиение на зоны.
влияет на точность прогноза, составленного с использованием этой модели. С точки зрения надежности и полезности модели притяжения и конфликтующих возможностей оказались примерно равноценными, хотя для последней, по-видимому, несколько проще проводить предварительное определение соответствующих параметров. В отличие от этих моделей эффективность метода Фратера проявилась лишь при анализе стабильных ситуаций. Если же за период прогноза происходили какие-либо изменения, например в характере использования городской территории, то метод Фратера оказывался совершенно непригодным. Что касается модели равных возможностей, то она по-настоящему не смогла конкурировать с тремя другими моделями, поскольку в рамках рассмотренной зональной структуры г. Вашингтона для нее невозможно было провести определение соответствующих параметров. Кроме того, значительное число небольших зон крайне затруднило установление оптимальных тарифов на проезд, что является серьезным недостатком модели равных возможностей, так как во многих исследованиях, связанных с использованием городской территории, необходимо рассматривать как раз весьма детальное разбиение на зоны.
Самое последнее достижение в области моделей распределения поездок представляет модификация модели притяжения, названная моделью максимизации энтропии [12].
1.4 Анализ распределения возможных видов транспортных средств
Данный этап исследования включает тщательный анализ состояния существующей транспортной сети. Основной целью такого анализа является сопоставление прогнозируемых потребностей в транспортном обслуживании с имеющимися в момент составления прогноза возможностями. По существу, на этом этапе решается вопрос, позволят ли изменения в организации сети и увеличение ее пропускной способности удовлетворить будущие потребности в перевозках людей и грузов.