Курсовая работа: Моделирование процессов статического конусообразования при разработке нефтяных, газовых и нефтегазовых залежей

2.3.1 Методика расчета предельных безводных и безгазовых дебитов, основанная на гидравлической теории безнапорного притока

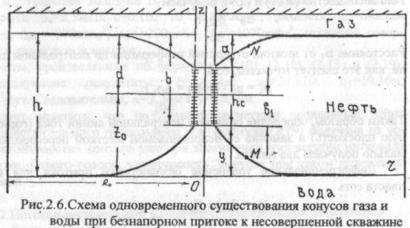
Схема одновременного существования газового и водяного конусов показана на рис.2.6. Пусть Нr, Нв, Нн есть гидравлические напоры в газовой, водяной и нефтяной зонах соответственно. Рr, Рв и Рн - пластовые давления в указанных зонах, а Р' - давление в некоторой точке на поверхности раздела газ-нефть и вода-нефть (см.рис.2.6), ρн, ρв, и ρr- плотности нефти, воды и газа соответственно. Тогда относительно точки N можно записать следующее выражение

Hr= ; HH= . (2.6)

Если эту точку переместить на контур скважины, то в соответствии с обозначениями на схеме имеем z=(h-b)+hc. Решая совместно два уравнения, исключая Р1 и пренебрегая капиллярным давлением РК=РН-РГ, получаем

HH = + (h - b+he) ; Δρ1 = ρH - ρr . (2.7)

Аналогично для точки М, перемещенной на контур скважины, получаем

Нв = - (h-b) ; Δρ2 = ρв – ρн

Если поместить точки N и М на контур пласта, то получаем, соответственно, выражения

Нн = + ; Hн = (2.8)

из которых следует

Нгρв = Нвρв – hΔρ1 (2.9)

Решая совместно (2.7), (2.8) и (2.9), находим нижнее положение интервала перфорации, обеспечивающее критическое значение безводного и безгазового дебита при заданном значении hc

b = h0 - (h-hc) ; Δρ3 = ρв-ρr. (2.10)

Определим ординату z0 нейтральной линии тока. Уравнения для напоров (2.7) и (2.8) относительно плоскости z0 (см.рис.2.6) записываются в виде:

Hн = + ; Нн = - (2.11)

Решая совместно (2.11) и (2.9), получаем

z0 = . (2.12)

Расстояние bi от нижних отверстий перфорации до нейтральной линии тока, как это следует из схемы, есгь

b1 = z0-(h - b) =. (2.13)

Таким образом, определив ординату нейтральной линии тока (горизонтальную плоскость) и заменив ее непроницаемой жесткой перегородкой, формально получаем два пласта.

Дифференциальное уравнение безнапорного притока для верхнего пласта есть

Q1 = . (2.14)

Разделяя переменные и интегрируя (2.14) в пределах по r от rс до R0 и по z от z2 до z1, где

z1 = h-z0;

z2 = hc- (2.15)

получаем

Q1 (h2-hc2)(l- )2 . (2.16)

Интегрируя уравнение для нижнего пласта, получаем