Курсовая работа: Моделювання бюджету доходів та витрат методом транспортної задачі
![]() . (1.5)
. (1.5)
Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (1.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою.
Планом транспортної задачі називають будь-який невід'ємний розв'язок системи обмежень (1.2) - (1.4), який позначають матрицею ![]() (
(![]() ). Значення невідомих величин
). Значення невідомих величин ![]() - обсяги продукції, що мають бути перевезені від
- обсяги продукції, що мають бути перевезені від ![]() -х постачальників до
-х постачальників до ![]() -х споживачів, називатимемо перевезеннями.
-х споживачів, називатимемо перевезеннями.
Оптимальним планом транспортної задачі називають матрицю ![]() (
(![]() ), яка задовольняє умови задачі, і для якої цільова функція (1.1) набирає найменшого значення.
), яка задовольняє умови задачі, і для якої цільова функція (1.1) набирає найменшого значення.
Теорема (умова існування розв'язку транспортної задачі): необхідною і достатньою умовою існування розв'язку транспортної задачі (1.1) - (1.4) є її збалансованість: ![]() .
.
Доведення. Необхідність. Нехай задача (1.1) - (1.4) має розв'язок ![]() , тоді для нього виконуються рівняння-обмеження (1.2) і (1.3). Підсумуємо відповідно ліві та праві частини систем рівнянь (1.2) і (1.3). Матимемо:
, тоді для нього виконуються рівняння-обмеження (1.2) і (1.3). Підсумуємо відповідно ліві та праві частини систем рівнянь (1.2) і (1.3). Матимемо:
![]() , (1.6)
, (1.6)
![]() . (1.7)
. (1.7)
Оскільки ліві частини рівнянь (1.6) та (1.7) збігаються, то праві також рівні одна одній, отже, виконується умова:
![]() . (1.8)
. (1.8)
Достатність. Потрібно показати, що за заданої умови (1.8) існує хоча б один план задачі, і цільова функція на множині планів обмежена.
Нехай ![]() . Розглянемо величину
. Розглянемо величину ![]() (
(![]() ). Підставивши значення
). Підставивши значення ![]() в систему обмежень задачі (1.1) - (1.4), матимемо:
в систему обмежень задачі (1.1) - (1.4), матимемо:
![]() ;
;
![]() .
.
Оскільки умови (1.2) та (1.3) виконуються, то ![]() (
(![]() ) є планом наведеної транспортної задачі.
) є планом наведеної транспортної задачі.
Виберемо з елементів ![]() (
(![]() ) найменше значення і позначимо його через
) найменше значення і позначимо його через ![]() . Якщо замінити в цільовій функції (1.1) всі коефіцієнти на
. Якщо замінити в цільовій функції (1.1) всі коефіцієнти на ![]() , то, враховуючи (1.2), функція набуває вигляд:
, то, враховуючи (1.2), функція набуває вигляд:
![]() .
.
Тобто цільова функція на множині допустимих планів транспортної задачі є обмеженою: ![]() . Теорему доведено.
. Теорему доведено.
Якщо при перевірці збалансованості (1.5) виявилося, що транспортна задача є відкритою, то її необхідно звести до закритого типу. Це здійснюється введенням фіктивного (умовного) постачальника ![]() у разі перевищення загального попиту над запасами (
у разі перевищення загального попиту над запасами (![]() ), із ресурсом обсягом
), із ресурсом обсягом ![]() . Якщо ж загальні запаси постачальників перевищують попит споживачів (
. Якщо ж загальні запаси постачальників перевищують попит споживачів (![]() ), то до закритого типу задача зводиться введення фіктивного (умовного) споживача
), то до закритого типу задача зводиться введення фіктивного (умовного) споживача ![]() з потребою
з потребою
![]() .
.
Вартість перевезення одиниці продукції від фіктивного постачальника ![]() (або фіктивного споживача
(або фіктивного споживача ![]() ) до кожного зі споживачів (виробників) має дорівнювати нулю або бути набагато більшою за реальні витрати
) до кожного зі споживачів (виробників) має дорівнювати нулю або бути набагато більшою за реальні витрати ![]() (
(![]() ). Як правило, у такому разі використовують нульові значення вартостей перевезень, що дає змогу спростити обчислення.
). Як правило, у такому разі використовують нульові значення вартостей перевезень, що дає змогу спростити обчислення.
Як згадувалося вище, транспортна задача (1.1) - (1.4) є звичайною задачею лінійного програмування і може бути розв'язана симплексним методом, однак особливості побудови математичної моделі транспортної задачі дають змогу розв'язати її простіше. Всі коефіцієнти при змінних у рівняннях (1.2), (1.3) дорівнюють одиниці, а сама система обмежень (1.2), (1.3) задана в канонічній формі. Крім того, система обмежень (1.2), (1.3) складається з mn невідомих та m+n рівнянь, які пов'язані між собою співвідношенням (1.8). Якщо додати відповідно праві та ліві частини систем рівнянь (1.2) та (1.3), то отримаємо два однакових рівняння:
![]() ;
; ![]() .
.
Наявність у системі обмежень двох однакових рівнянь свідчить про її лінійну залежність. Якщо одне з цих рівнянь відкинути, то в загальному випадку система обмежень буде містити ![]() лінійно незалежне рівняння, отже, їх можна розв'язати відносно
лінійно незалежне рівняння, отже, їх можна розв'язати відносно ![]() базисних змінних. Опорний план транспортної задачі такий допустимий її план, що містить не більш ніж
базисних змінних. Опорний план транспортної задачі такий допустимий її план, що містить не більш ніж ![]() додатних компонент, а всі інші його компоненти дорівнюють нулю. Такий план є невиродженим. Якщо ж кількість базисних змінних менша ніж
додатних компонент, а всі інші його компоненти дорівнюють нулю. Такий план є невиродженим. Якщо ж кількість базисних змінних менша ніж ![]() , то маємо вироджений опорний план.
, то маємо вироджений опорний план.
1.2 Методи розв’язання транспортної задачі
Один із способів розв’язування транспортної задачі ґрунтується на розгляді двоїстої задачі.
Розглянемо транспортну задачу (1.1-1.4). Позначимо змінні двоїстої задачі, які відповідають рівнянням (1.2), через ![]() , а для рівнянь (1.3) - через
, а для рівнянь (1.3) - через ![]() . Оскільки всі обмеження транспортної задачі є рівняннями, то пара спряжених задач є несиметричною і ніякі обмеження на знаки змінних двоїстої задачі
. Оскільки всі обмеження транспортної задачі є рівняннями, то пара спряжених задач є несиметричною і ніякі обмеження на знаки змінних двоїстої задачі ![]() та
та ![]() не накладаються.
не накладаються.
Для побудови двоїстої задачі поставимо у відповідність обмеженням початкової задачі змінні двоїстої:
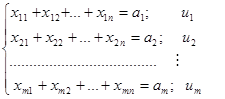 (1.9),
(1.9),
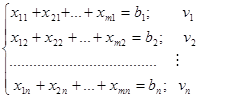
![]() (1.10),
(1.10), ![]()