Курсовая работа: Моделювання надходження повідомлень від датчиків до ЕОМ

REM. – число одиниць вільного обсягу пам'яті в кінці періоду моделювання;

MIN. – мінімальна кількість використовуваних одиниць пам’яті за період моделювання;

MAX. – максимальна кількість використовуваних одиниць пам'яті за період моделювання;

ENTRIES – кількість входів на згадку за період моделювання;

AVL. – стан готовності пам'яті наприкінці періоду моделювання;

AVE.C. – середнє число зайнятих одиниць пам'яті за період моделювання;

UTIL. – частина періоду моделювання, протягом якого пам'ять використовувалася;

RETRY – кількість транзактів, що очікують спеціальних умов, що залежать від стану пам'яті;

DELAY – кількість транзактів, що очікують можливості входу в блок ENTER.

6 Перевірка адекватності моделі системи обробки повідомлень від датчиків та вимірюючих пристроїв на ЕОМ

Для перевірки імітаційної моделі, дещо змінимо текст програми, видаливши перевірку часу актуальності повідомлень і змінивши заданий рівномірний закон надходження повідомлень від датчиків та їх обробки на експоненційний закон (текст даної програми для виконання верифікації показаний в додатку В).

Це дозволить перевірити відповідність результатів моделювання видозміненої моделі (результати моделювання видозміненої моделі приводяться в додатку Г) характеристикам, які можна отримати за допомогою математичних формул які отримані для відповідної, еквівалентній даній моделі, найпростішої одноканальної СМО з обмеженою довжиною черги. Інтервали часу між заявками є незалежними і мають паусонівський (найпростіший) розподіл випадкових величин, які утворюють стаціонарний потік[1]. Для цього потоку число заявок k для будь-якого інтервалу часу має розподіл за експоненційним законом. Закон описується формулою і дозволяє обчислити ймовірність надходження k заявок за інтервал часу t.

Для найпростішого потоку з інтенсивністю λ інтервал t між сусідніми подіями має показниковий розподіл з щільністю:

.

Графік функції розподілу показаний на рисунку 3.

Рисунок 3 — Графік щільності ймовірності експоненційного розподілу

Знайдемо вигляд закону розподілу:

Графік функції розподілу представлений на рисунку 4.

Рисунок 4 — Графік експоненційного розподілу

Відповідні математичні формули для розрахунку такої найпростішої одноканальної СМО з відомою довжиною черги подаються нижче.

Кількість втрачених повідомлень розраховується за формулою[3]:

(1),

де N – загальна кількість повідомлень, n – довжина черги, а ρ розраховується за формулою . Так як інтенсивність потоку надходження , а інтенсивність потоку обробки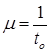 , то ρ розраховується за формулою:

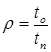(2),

де t_o - час обробки повідомлень на ЕОМ, t_n – інтервал надходження інформації від датчиків та вимірювальних пристроїв

Кількість оброблених повідомлень:

Nобр=Np–Nвтр (3).

Підставивши в формулу (2) задані значення t_o =7 секунди і t _n =8 секунд (λ=1/7, μ= 1/8), отримаємо ρ= 0.875. Після підстановки в формулу (1) задане значення N=440, n=1 і розраховане значення ρ= 0.875 отримаємо теоретичну кількість втрачених повідомлень - Nвтр=167. Підставивши це значення в формулу (3) отримаємо теоретичну кількість оброблених повідомлень: Nобр=270 повідомлень.