Курсовая работа: Моделювання транспортної мережі

Цей алгоритм більш загальний у порівнянні з алгоритмом Дейкстри, тому що він знаходить найкоротші шляхи між будь-якими двома вузлами мережі. У цьому алгоритмі мережа представлена у виді квадратної матриці з рядками і стовпцями. Елемент дорівнює відстані від вузла до вузла , що має кінцеве значення, якщо існує дуга , і дорівнює нескінченності в противному випадку.

Покажемо спочатку основну ідею методу Флойда. Нехай є три вузли і задані відстані між ними (рис. 3.1). Якщо виконується нерівність , то доцільно замінити шлях шляхом . Така заміна (далі її будемо умовно називати трикутним оператором ) виконується систематично в процесі виконання алгоритму Флойда.

Рис. 3.1. Трикутний оператор

Алгоритм Флойда вимагає виконання наступних дій.

Крок 0 . Визначаємо початкову матрицю відстаней і матрицю послідовності вузлів . Діагональні елементи обох матриць позначаються знаком «–», що показує, що ці елементи в обчисленнях не беруть участь. Думаємо :

Рис. 3.2. Початкова ситуація

Основний крок k . Задаємо рядок і стовпець як ведучий рядок і ведучий стовпець . Розглядаємо можливість застосування трикутного оператора до всіх елементів матриці . Якщо виконується нерівність , тоді виконуємо наступні дії:

· створюємо матрицю шляхом заміни в матриці елемента на суму ,

· створюємо матрицю шляхом заміни в матриці елемента на . Думаємо і повторюємо крок .

Пояснимо дії, виконувані на -м кроці алгоритму, представивши матрицю так, як вона показана на рис 3.3. На цьому рисунку рядок і стовпець є ведучими. Рядок – будь-який рядок з номером від 1 до , а рядок – довільний рядок з номером від до . Аналогічно стовпець представляє будь-як стовпець з номером від 1 до , стовпець – довільний стовпець з номером від до . Трикутний оператор виконується в такий спосіб. Якщо сума елементів ведучих рядка і стовпця (показаних у квадратах) менше елементів, що знаходяться в перетинанні стовпця і рядка (показаних у кружках), що відповідають розглянутим ведучим елементам, то відстань (елемент у кружку) заміняється на суму відстаней, представлених ведучими елементами:

Рис. 3.3. Ілюстрація алгоритму Флойда

Після реалізації кроків алгоритму визначення по матрицях і найкоротшому шляху між вузлами і виконується за наступними правилами.

1. Відстань між вузлами і дорівнює елементові в матриці .

2. Проміжні вузли шляху від вузла до вузла визначаємо по матриці . Нехай , тоді маємо шлях . Якщо далі і , тоді вважаємо, що весь шлях визначений, тому що знайдені всі проміжні вузли. У противному випадку повторюємо описану процедуру для шляхів від вузла до вузла і від вузла до вузла .

При аналізі транспортних мереж часто виникає задача визначення максимального потоку, що може пропустити дана мережа, а також задача розподілу цього потоку по дугах мережі.

З математичної точки зору задача про максимальний потік формулюється в такий спосіб: при заданій конфігурації мережі і відомої пропускної здатності знайти ненегативні значення , що задовольняють умовам і, що максимізують функцію , тобто

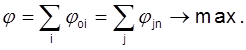
Алгоритм для знаходження максимального потоку був запропонований Фордом і Фалкерсоном і полягає в поступовому збільшенні потоку, що пропускається по мережі, доти, поки він не стане найбільшим. Алгоритм заснований на теоремі Форда-фалкерсона: у будь-якій транспортній мережі максимальний потік із джерела в стік , дорівнює мінімальній пропускній здатності розрізу, що відокремлює від .

Крок 0 . Призначаємо вузлові 15 постійну мітку [0, -].

Крок 1 . З вузла 15 можна досягти вузлів 21 2 12. Обчислюємо мітки для цих вузлів, у результаті одержуємо наступну таблицю міток:

Вузол	Мітка	Статус мітки
15		Постійна
« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 452 Бесплатно скачать Курсовая работа: Моделювання транспортної мережі >>> Скачать <<< Меню Поиск