Курсовая работа: Наближені методи розв’язку нелінійних рівнянь
Алгоритм розв’язку цього ж рівняння за методом простої ітерації полягає в тому, що спочатку вихідне рівняння потрібно привести до вигляду x=g(x), тобто виразити х з рівняння, а потім використовуючи формулу x1 =g(x0 ), де відповідно х1 – значення х на наступній ітерації, а х0 – значення х на попередній ітерації. Знаходимо також ряд х до тих пір, поки не виконається умова ![]() < Δ, де Δ - задана допустима похибка.
< Δ, де Δ - задана допустима похибка.
Блок схеми методів наведені в додатку А.
Вибір інструментальних засобів
Для вирішення цієї задачі було обрано середовище програмування С, так як воно має ряд вагомих переваг перед іншими середовищами і мовами програмування. Зокрема такими перевагами є те, що:
- не вимагає великих затрат як апаратної частини комп’ютера так і програмної.
- Дозволяє досить просто реалізовувати поставлені задачі
- Є дуже візуальним і наглядним що робить його зручним інструментом в користуванні.
- Ця мова є досить гнучка і дозволяє використовувати технології об’єктно-орієнтованого програмування.
Вхідні та вихідні дані
Вхідними даними для програми є :
1)Для методу Ньютона: початкове рівняння; похідна від нього; початкове
наближення (х0 ) і допустима, задана за умовою
задачі похибка.
2)для методу простої ітерації: початкове рівняння, приведене до вигляду
x=g(x); початкове наближення і допустима
похибка.
Вихідними даними для обох методів є значення х, яке задовольняє умову![]() < Δ, де Δ – задана за умовою похибка.
< Δ, де Δ – задана за умовою похибка.
Структура програми
Програма розділена на чотири частини такі як:
1) блок опису вхідних та вихідних даних;
2) введення початкових даних;
3) виклик підпрограм для розв’язок задачі різними методами (в даному випадку методом Ньютона та методом простої ітерації);
4) виведення результатів;
інструкція користувачеві
Для запуску програми необхідно запустити файл з назвою “метод Ньютона та простої ітерації ” після чого на вашому екрані відкриється вікно програми (рисунок 7.1).
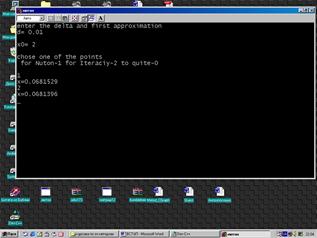
Рисунок 7.1
Необхідно слідувати вказівкам які з’явились у робочому вікні програми, а саме спочатку ввести допустиму похибку – dпотім – початкове наближення – х0 після чого потрібно обрати метод (Ньютона чи простої ітерації) яким ви бажаєте розв’язати дане рівняння, тобто згідно інструкції натисніть 1 для того щоб розв’язати рівняння методом Ньютона або 2 – для методу простої ітерації, потім натисніть кнопку Enter і ви побачите результат. Наприклад: х=0,0681529 (рисунок 1.). після того як ви отримали результат якимось одним методом ви також відразу можете отримати його і іншим відповідно вибравши 1 чи 2 для методу який вас цікавить.
Аналіз результатів розрахунку
Отже після проведення розрахунку по знаходженню коренів нелінійного рівняння за методами Ньютона та простої ітерації отримано наступні результати: рівняння має 5 коренів, а саме один дійсний і чотири комплексні: хдійсне.Нютона =0,0681529, хкомпл.1,2 = -0,9+ 1,8і; хкомпл.3,4 = -1,4+ 1,34і;хдійс.пр.ітерації =0,0681396. Порівнявши отримані результати з наступними результатами
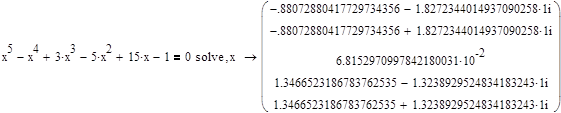 ,
,
що отримані за допомогою автоматизованого математичного пакету Mathcad, можна зробити висновок що корені рівняння розраховані за допомогою чисельних методів є досить таки точними і похибка складає не більше 0.01. за отриманими результатами також можна зробити висновок щодо швидкодії кожного з методів, а саме при однакових початкових умовах метод простої ітерації працює дещо швидше, ніж метод Ньютона, але точніший результат дає метод Ньютона.
Ця курсова робота була присвячена розв’язанню нелінійних рівнянь методами Ньютона та простої ітерації. В результаті роботи було досліджено існуючі методи для розв’язання таких рівнянь, а більш детально розглянуті вищезгадані два методи, а саме Ньютона та простої ітерації. Для цих методів було складено блок-схему, а також написано програму. В результаті роботи за допомогою складеної програми було отримано певні корені заданого рівняння і порівняно їх з значеннями коренів цього ж рівняння, але розв’язаного за допомогою спеціалізованого математичного програмного пакету Mathcad.
Література
1. Квєтний Р. Н. Методи комп’ютерних обчислень. – Навчальний посібник. – Вінниця: ВДТУ, 2001.