Курсовая работа: Нахождение оптимального плана производства продукции с использованием пакетов прикладных программ
![]()
При следующей системе ограничений:
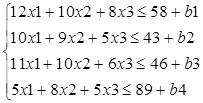
При чем: 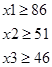
Распределение денежных средств на пять лет (в рублях): 80 000, 100 000, 110 000, 120 000, 150 000.
ГЛАВА 2. ОЗНАКОМИТЕЛЬНЫЙ КУРС ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
Введение
В мире деятельность практически всегда не просто осознанная, а целенаправленная, какая-то работа совершается ради достижения определенной цели. Конечно, практически всегда ресурсы, необходимые для выполнения данной работы, ограничены. Достаточно часто существует несколько возможностей распорядится ресурсами, и хотелось бы сделать это каком-то смысле «получше». Исследование операций как раз и занимается этим кругом вопросом: цель работы – ограниченность необходимых ресурсов – поиск вариантов возможных решений – определение способа действий. Цель - это желаемый результат деятельности.
Линейное программирование
Экономико-математическая модель есть математическое описание, закономерности исследуемого экономического процесса или объекта.
Задачами линейного программирования (ЛП) являются такие оптимизационные задачи, в которых целевая функция и функциональные ограничения - линейные функции относительно переменных, принимающих любые значения из некоторого множества значений.
Стандартная задача линейного программирования записывается в виде:
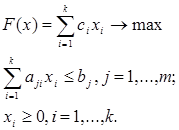
В задаче линейного программирования нестрогие функциональные неравенства можно превратить в строгие равенства, добавив неизвестные неотрицательные дополнительные переменные. Конечно, число неизвестных и число уравнений в системе могут быть разными. Но и в этом случае из курса линейной алгебры для системы уравнений известны варианты: система может быть несовместной, то есть не иметь решений вообще; решение может быть одно, но (!) это единственное решение может оказаться недопустимым из-за наличия отрицательных компонентов в решении; решений может быть бесконечно много. Вообще же для единственности решения задачи ЛП не требуется равенства числа переменных и числа ограничений (нестрогих неравенств). Для задач ЛП разработаны многочисленные эффективные методы решения и соответствующее математическое обеспечение для различных ситуаций.
Эквивалентность задач линейного программирования
1. Задачу максимизации можно свести к задаче минимизации и наоборот:
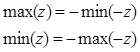
2. Любое неравенство можно представить в виде равенства путем введения дополнительной отрицательной переменной.
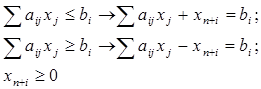
3. Переменную, не ограниченную условием неотрицательности можно заменить разностью двух неотрицательных переменных:
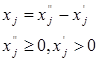
4. Любое равенство можно представить как систему двух неравенств:
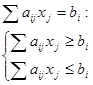
Геометрическая интерпретация задач ЛП
Любое неравенство определяет полупространство. Система неравенств определяет пересечение многих пространств. В результате с учетом условий неотрицательности переменных область допустимых решений – ОДР представляет собой многогранник. Любая точка многогранника является допустимым решением ЗЛП. Линейная целевая функция достигает экстремума на выпуклом множестве (многограннике) только на границе. Любые переменные плоскости целевой функции, параллельно самой себе, есть лишь изменение значений целевой функции. Два крайних положения этой плоскости в ОДР являются точками экстремума.
Алгоритм симплекс-метода
Симплекс – простейший многогранник. Метод состоит из двух основных этапов:
1. Нахождение допустимого решения.
2. Нахождение оптимального решения среди допустимых решений.
Решение симплекс-методом сопровождается так называемой симплекс-таблицой. На основе анализа таких таблиц определяется необходимость улучшения решения или отсутствие решения или нахождение оптимального решения.
Первым делом необходимо получить каноническую задачу. Преобразование общей и стандартной ЗЛП производится на основе свойств эквивалентности этих задач. При этом неравенство преобразуется в равенство путем введения дополнительной неотрицательной переменной. В результате система ограничений будет записана в виде системы линейных уравнений, где количество неизвестных больше, чем количество уравнений.