Курсовая работа: Нахождение оптимального плана производства продукции с использованием пакетов прикладных программ
На основании полученных выражений для базисных переменных из целевой функции исключаются все базисные переменные. Составляется симплекс- таблица по следующим правилам:
1. Первый столбец включает базисные переменные.
2. Составляется второй столбец из свободных членов.
3. Последующие столбцы составляются из коэффициентов при свободных переменных с противоположными знаками.
4. Последней строкой этой таблицы является строка целевой функции.
| Базисные переменные | Свободные члены | Свободные переменные | |||||
| x1 | x2 | … | xj | … | xn | ||
| Xn+1 | b1 | A11 | A12 | … | A1j | … | A1n |
| Xn+2 | b2 | A21 | A22 | … | A2j | … | A2n |
| ... | … | … | … | … | … | … | … |
| Xn+i | bi | Ai1 | Ai2 | … | Aij | … | Ain |
| … | … | … | … | … | … | …. | … |
| Xn+m | bm | Am1 | Am2 | … | Amj | … | Amn |
| z | 0 | -c1 | -c2 | …. | -cj | … | -cn |
Базисное решение – это решение системы линейных уравнений относительно базисных переменных, когда свободные переменные равны нулю. Все базисные переменные равны свободным членам в первой симплекс-таблице.
![]()
Признак допустимости базисных решений
- базисное решение допустимое, если оно неотрицательное;
- базисное решение допустимое, если в столбце свободных членов нет ни одного отрицательного элемента (кроме строки целевой функции).
Признак несовместимости ограничений
Ограничения несовместны, если в каждой строке, имеющей отрицательный свободный член, нет ни одного отрицательного элемента( Этот признак используется, если решение недопустимое).
Признак оптимальности
Если в строке целевой функции все элементы одного знака (кроме свободного члена), то целевая функция принимает экстремальное значение, при чем, если все элементы положительны, то - max, если отрицательны – min.
Признак неограниченности целевой функции
Целевая функция неограничена, если в любом столбце, не удовлетворяющим признаку оптимальности, нет ни одного положительного элемента, при чем не ограничена сверху при нахождении максимума; и целевая функция не ограничена снизу при нахождении минимума, если в любом столбце, имеющем положительный элемент в строке целевой функции, нет ни одного отрицательного элемента.
Признак существования альтернативного (неединственного) решения
Оптимальное решение имеет альтернативу, если в строке целевой функции есть нулевые элементы (кроме свободных членов).
Нахождение разрешающих элементов
Разрешающий элемент находится на пересечении разрешающей строки и разрешающего столбца. Разрешающая строка указывает на базисную переменную, переходящую в свободную. Разрешающий столбец указывает на свободную переменную, переходящую в базисную.
1. Разрешается столбец.
a) решение недопустимое: в любой строке, имеющей отрицательный свободный член, находится отрицательный элемент. Этот элемент находится в разрешающем столбце.
b) решение допустимое, неоптимальное: любой столбец, не удовлетворяющий признаку оптимальности, является разрешающим столбцом.
2. Разрешающая строка.
Находятся положительные отношения свободных членов к элементам разрешающего столбца. Минимальное отношение соответствует разрешающей строке.
Правила преобразования симплекс-таблицы
1. В новой таблице меняются местами по разрешающему элементу свободные и базисные переменные:
![]()
2.Ячейка разрешающего элемента заполняется обратным знаком:
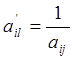
3. Разрешающая строка делится на разрешающий элемент: