Курсовая работа: Научная полемика в исследовании систем управления
ПФ называется динамической, если: а) время t фигурирует в качестве самостоятельного фактора производства, влияющего на объем выпускаемой продукции; б) параметры ПФ и ее характеристика f зависят от времени t, если параметры ПФ оцениваются по данным временных рядов (объем ресурсов и выпуска) продолжительностью tо лет (т. е. базовый промежуток для оценки параметров имеет продолжительность tо лет), то экстраполяцию по такой производственной функции следует рассчитывать не более чем на tо/3 лет вперед (т. е. промежуток экстраполяции должен иметь продолжительность не более чем tо/3 лет).
При построении ПФ влияние НТП учитывается множителем ept , где р (р > 0) — характеризующий темп прироста выпуск, осуществляемый под влиянием НТП:
у (t)=ept f(x1 (t), x2 (t)),
где t = 0,1,..., Т.
Данная ПФ — простейшая динамическая ПФ, содержащая нейтральный (не материализованный в одном из факторов) технический прогресс. В сложных случаях НТП, выступающий как трудо- или капиталосберегающий фактор, может воздействовать непосредственно на производительность и капиталоотдачу:
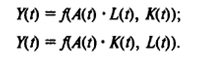
В целом выбор аналитической формы ПФ у=f(x1 , x2 ) обусловливается теоретическими соображениями учета особенностей взаимосвязей между конкретными ресурсами (при микроэкономическом уровне), особенностей параметризации (реальных или экспертных данных, преобразуемых в параметры ПФ). Отметим, что оценка параметров ПФ обычно проводится с помощью метода наименьших квадратов.
Производственная функция f(x1 , x2 ) должна удовлетворять ряду свойств[13] :
а) без ресурсов нет выпуска;
б) с ростом затрат хотя бы одного ресурса объем выпуска растет;
в) с ростом затрат одного (i-го) ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу j-го ресурса не растет (закон убывающей эффективности);
г) производственная функция является однородной функцией степени р > 0: при р > I с ростом масштаба производства в г раз (t > 1) объем выпуска возрастает в tP раз (т. е. имеем рост эффективности производства при росте масштаба производства); при р < I имеем падение эффективности производства от роста масштаба производства; при р-\— постоянную эффективность производства при росте его масштаба или независимость удельного выпуска от масштаба производства.
Ошибочность исходной гипотезы о степени взаимозаменяемости факторов может служить причиной недостаточной статистической значимости оценок производственной функции Кобба—Дугласа.
Линейное программирование — это частный раздел оптимального программирования. В свою очередь оптимальное (математическое) программирование — раздел прикладной математики, изучающий задачи условной оптимизации. В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении.
Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Именно такие ситуации, как правило, и составляют повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и т.д.).
Слова «наилучшим образом» здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум рентабельности» и др.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными —
а) линейные,
б) нелинейные.
В случае а) все функциональные связи в системе ограничений и функция цели — линейные функции; наличие нелинейности хотя бы в одном из упомянутых элементов приводит к случаю б).
2. По характеру изменения переменных —
а) непрерывные,
б) дискретные.
В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения.
3. По учету фактора времени —
а) статические,
б) динамические.