Курсовая работа: Нейронні мережі нового покоління

7. Вибір найкращої хромосоми

Розглянемо ГА більш детально:

1. Ініціалізація, або вибір початкової популяції хромосом. Полягає у випадковому виборі заданої кількості N хромосом (особин).

2. Оцінювання пристосованості хромосом в популяції полягає у розрахунку функції пристосованості для кожної хромосоми p_S (X_i ). Приймається, що функція пристосованості завжди приймає невід’ємні значення. Звичайно знаходиться максимум цієї функції.

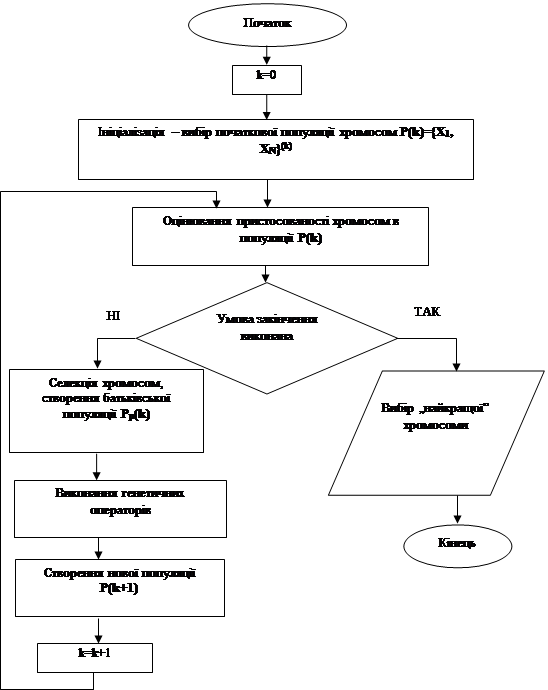Рис.2.1 Алгоритм класичного ГА.

3. Перевірка умови закінчення алгоритму. Алгоритм може бути закінчений, якщо його виконання не приводить до покращення отриманого результату або через певний проміжок часу. .

4. Селекція хромосом полягає у виборі на основі функції пристосованості тих хромосом, які будуть приймати участь у створення нащадків, тобто нового покоління. Такий вибір виконується згідно принципу природного відбору, за яким найбільші шанси на створення потомства мають хромосоми з найвищими значеннями функції пристосованості. Існують різні методи селекції. Найбільш популярним вважається метод рулетки. Кожній хромосомі ставиться у відповідність сектор колеса рулетки, величина якого пропорційна до функції пристосованості даної хромосоми. Ймовірність селекції хромосоми X_i , i=1. N (для випадку, що функція F максимізується):

.

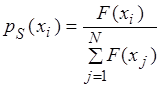Таким чином, ймовірність селекції найбільша для хромосом з великим значенням функції пристосованості. У результаті селекції формується батьківська популяція з чисельністю N у яку особини з великим значенням p_S (X_i ) можуть увійти кілька разів, а з малим значенням p_S (X_i ) - жодного.

5. Використання генетичних операторів до відібраних у результаті селекції батьківських хромосом приводить до створення популяції нащадків. В класичному ГА використовують два основних генетичних оператора: оператор схрещування (crossover ) і оператор мутації (mutation ). Як і живих організмах, ймовірність мутації звичайно дуже мала (р_м <0,1).

В ГА мутація може виконуватися на популяції батьків перед схрещуванням або на популяції нащадків, утворених у результаті схрещування.

Оператор схрещування . На першому етапі схрещування вибиваються пари хромосом з батьківської популяції. Операції схрещування полягають у обміні фрагментами ланцюжків між двома батьківськими хромосомами (рис.2.2). Далі для кожної пари вибирається позиція гена (локус ) в хромосомі, який визначає точку схрещування. Якщо хромосома містить L двійкових чисел, то точка схрещування L_K вибирається випадковим чином з інтервалу [1, L]. В результаті схрещування утворюються два нащадки:

1) нащадок, хромосома якого на позиціях від 1 до L_K складається з генів першого предка, а позиції від L_K +1 до L - з генів другого предка.

2) нащадок, хромосома якого на позиціях від 1 до L_K складається з генів другого предка, а позиції від L_K +1 до L - з генів першого предка.

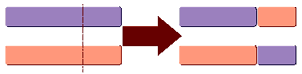
Рис.2.2 Умовна схема кросовера

6. Формування нової популяції. Хромосоми, отримані у результаті генетичних операторів до популяції предків, утворюють нову популяцію. Така популяція стає поточної для даної ітерації k ГА. На кожній ітерації розраховується значення функції пристосованості для всіх хромосом. В результаті перевірки умови закінчення ітерацій відбувається або зупинка алгоритму, або перехід до нового кроку ГА - селекції. В результаті селекції вся попередня популяція замінюється популяцією нащадків з кількістю N. Етап схрещування і мутації також називається еволюцією, на якому відбувається рекомбінація генів у хромосомах.

7. Вибір найкращої хромосоми. Найкращою вважається хромосома з максимальним значенням функції пристосованості.

Головний фактор еволюції - природний відбір, тобто природна селекція, приводить до того, що виживають найбільш пристосовані особини.

Генетичний алгоритм є комбінованим методом. Механізми схрещування і мутації в якомусь значенні реалізують переборну частину методу, а відбір кращих рішень - градієнтний спуск. Така комбінація дозволяє забезпечити стійко хорошу ефективність генетичного пошуку для будь-яких типів задач.

2.2.4 Нечіткі системи

За допомогою нечітких множин можна формально визначити неточні та багатозначні поняття, такі як "висока температура", "молодий чоловік", "середній зріст" або "велике місто" [3]. Перед формулюванням визначення нечіткої множини необхідно задати так звану область значень (universe of discourse ). В випадку неоднозначного розуміння "багато грошей" великою буде визнана одна сума, якщо ми обмежимось діапазоном [0, 1000 грн.] та зовсім інша в діапазоні [0, 1000000 грн.]. Область значень, далі будемо називати простором або множиною , буде позначатись символом Х . Необхідно пам’ятати, що Х - чітка множина.

Визначення. Нечітка множина А в деякому (не порожньому) просторі Х , що позначається як А ÍХ , називається множиною пар

A = { (x,m_A (x)); x ÎX } (2.1)

де

m_A : X ® [0,1] (2.2)

функція приналежності нечіткої множини А . Ця функція приписує кожному елементу х ÎХ степінь його приналежності до нечіткої множини А , при цьому можна виділити три випадки:

1) m_A (x) = 1 означає повну приналежність елемента х до нечіткої множини А , тобто х ÎА ;

2) m_A (x) = 0 означає відсутність приналежності елемента х до нечіткої множини А, тобто х ÏА ;

3) 0 < m_A (x) < 1 означає часткову приналежність елемента х до нечіткої множини А .