Экономико-математическое моделирование / Курсовая работа: Некоторые аспекты моделирования конкурентного равновесия

Курсовая работа: Некоторые аспекты моделирования конкурентного равновесия

В модели Вальраса считается, что весь доход производственного сектора полностью распределяется между потребителями:

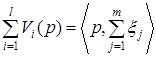
где , а скалярное произведение справа, с учетом структуры векторов , трактуется как прибыль всего производственного сектора. Заметим, что суммирование векторов осуществляется покомпонентно.

Функции спроса , и предложения , предполагаются векторными и множественнозначными. Например, для функции первое свойство означает, что , где - скалярная функция спроса на k‑ый товар. Второе свойство означает, что функция каждому p ставит в соответствие не один вектор , а множество таких векторов, т.е. . Это имеет место когда максимум спроса достигается не только в одной точке.

В модели Вальраса понятия совокупных спроса и предложения формализуются следующим образом.

Определение 2.1. Функцией совокупного (рыночного) спроса называется множественнозначная функция

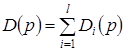(2.3)

Функцией совокупного (рыночного) предложения называется множественнозначная функция

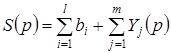(2.4)

Введем обозначения:

, ,

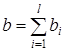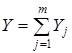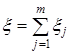
По определению, любой элемент множества Y можно представить вектором , где . Так как есть множество оптимальных планов производителя j, то компонентами вектора являются оптимальные объемы выпуска и затрат, и все они составляют решение одной и той же оптимизационной задачи. Таким образом, часть компонент вектора , как и векторов , отражает предложение готовых продуктов, а часть – спрос на первичные факторы. Поэтому вектор нельзя называть однозначно предложением. В то же время, вектор может быть интерпретирован как совокупное предложение, так как часть компонент вектора , соответствующая спросу, «компенсируется» вектором b.

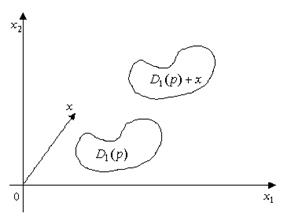
Рис. 2. Сумма вектора и множества.

Покажем, что для любого p и , т.е. областью изменения совокупных функций является то же самое пространство, что и для индивидуальных функций. Рассмотрим сначала двух потребителей. Для любого множество образуется смещением множества в направлении вектора x на длину этого вектора (рис. 2). Поэтому:

Рассмотрим трех потребителей. Для любого множество образуется смещением множества в направлении вектора x на длину этого вектора. Поэтому:

Продолжая эти рассуждения, получаем

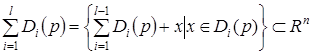
Точно так же устанавливается включение . Так как и потому , то множество b+Y образуется смещением множества Y в направлении вектора b на длину этого вектора. Поэтому .

Формализовав понятия функций совокупных спроса и предложения, модель рынка (2.1) можно представить совокупностью вида

(2.5)

Любой вектор называется совокупным спросом (соответствующим вектору цен p); любой вектор – совокупным предложением (соответствующим вектору цен p). Эти векторы являются (оптимальными) реакциями совокупного покупателя и совокупного продавца на установившийся на рынке вектор цен. Если при этом , то на рынке возникает дефицит товаров, а при появляются их излишки. Такие цены не могут считаться удовлетворительными, так как в одном случае ущемлены интересы покупателей, а в другом – продавцов. Очевидно, наилучшим вариантом для экономики является равенство . Этот идеальный случай на практике не всегда имеет место. Поэтому целесообразно как-то его ослабить. В модели Вальраса допускается наиболее «гуманный» с точки зрения интересов потребителей вариант обобщения понятия экономического равновесия.