Курсовая работа: Новое объяснение релятивистских явлений
Все инерциальные системы равноправны и время в них едино, т.е. одинаково, и меняется в одном темпе (ньютоновское абсолютное время). Замедление времени это явление, обусловленное эффектом Доплера. То же самое имеет место для сокращения отрезка. Пространство является общим и евклидовым для всех инерциальных систем отсчета. Сокращение отрезка есть явление, обусловленное различием ориентации фронта световой волны в сравниваемых инерциальных системах отсчета.
Эйнштейн и апологеты его теории не были последовательны в своих высказываниях. 4-пространство-время манило их, но вело к неразрешимым парадоксам (логическим противоречиям). Чтобы «избавиться» от них апологеты проявляли непоследовательность, то, утверждая первый вариант, то «скатываясь» ко второму, и в то же время не признавая ни единства времени, ни общего пространства для всех инерциальных систем.
Для иллюстрации процитируем одного из популяризаторов СТО (на популяризацию СТО и объяснение парадоксов мало кто отваживается) [7]:
«... Часто говорят, интерпретируя полученный результат, что движущиеся часы идут медленнее неподвижных. Нельзя не признать эту фразеологию крайне неудачной. Дело в том, что часы во всех ИСО идут совершенно одинаково. Различным оказывается отсчет промежутков времени между событиями».
Мы специально выделили жирным шрифтом в цитате признание единства времени, т.е. признание второго варианта. Но в том же учебнике читаем [7]:
«... современная физика отказалась от абсолютного пространства и времени... Современная физика пришла к заключению, что время течет по-разному в разных системах отсчета».
Сказав «а», автор боится сказать «б», т.е. словесно объявляет свою приверженность первому варианту. Вот вам пример логической непоследовательности в объяснении релятивистских явлений. В.Г.Левич твердо стоит на первом варианте, но не «спускается» до объяснений [2]:
«Движущиеся часы ... идут медленнее, чем часы, покоящиеся в этой системе отсчета ... Не существует универсального мирового времени».
Логических противоречий, возникающих при использовании принципа Галилея – Пуанкаре, он «не видит». Теперь процитируем объяснение «сжатия» движущегося отрезка [7]:
«Часто спрашивают: чему равна длина линейки «на самом деле»? Этот вопрос лишен смысла, если задавать его «вообще». В каждой системе отсчета линейка имеет свою длину; это и есть ее длина «на самом деле». Все системы равноправны и все определяемые в этих системах длины линейки также равноправны... Для линейки существует все же одна «избранная» система координат, а именно та, в которой она покоится».
Вот вам «равноправие» инерциальных систем на словах и «избранная» система на деле!
2. Теория, изъеденная парадоксами
Как только Эйнштейн принял концепцию действительного замедления времени и действительного сокращения пространства в направлении движения и одновременно продекларировал равноправие инерциальных систем отсчета, «парадоксы» (логические противоречия) посыпались как из рога изобилия.
Рассмотренные нами два парадокса Эйнштейн относил к кинематическим, т.е. обусловленным относительным движением инерциальных систем. К кинематическим эффектам относится и большая группа парадоксов, связанных с вращательным движением, о которой в учебниках и книгах вообще стараются не упоминать. Рассмотрим несколько таких парадоксов (нелепостей СТО).
Пусть неподвижное кольцо расчерчено радиальными линиями, число которых No =1000 (см. рис.1, левое кольцо). Будем постепенно увеличивать скорость вращения кольца. Благодаря «лоренцеву сокращению» расстояние между линиями будет уменьшаться в (1–v2 /c2 )1/2 раз. Когда скорость достигнет v=0,045с, мы сфотографируем вращающееся кольцо. Сколько линий окажется на фотографии No =1000 или же N=1001?
Если No = 1000, то «лоренцево сокращение» отсутствует, т.е. Специальная теория относительности дает неверный результат (лжет).
Если N = 1001, тогда возникает проблема: какая линия сфотографировалась дважды?
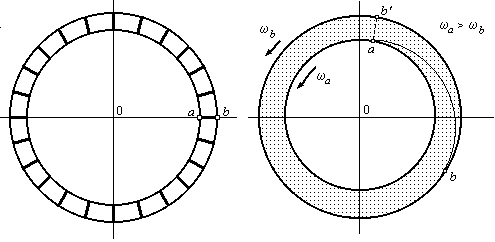
Рис. 1. Парадоксы вращающегося кольца
Рассмотрим другой вариант парадокса с этим кольцом. Согласно Специальной теории относительности внешний (периферийный) край кольца должен иметь меньшую угловую скорость, чем внутренний (см. рис.1, правое кольцо). По этой причине точка «a» кольца будет «убегать» относительно точки «b». Линия ab окажется уже не радиальной (как в классической механике ab'), а будет с течением времени удлиняться, напоминая кольцевую спираль, число витков которой постоянно растет. Если мы быстро остановим кольцо, как будет вести себя эта спираль? Сразу станет «радиальным отрезком» или же будет некоторое время «раскручиваться»? Будет ли наблюдатель, вращающийся вместе с кольцом, наблюдать этот эффект?
Парадоксы вращательного движения имеют давнюю историю. Процитируем историю «парадокса Эренфеста» [3]:
«Суть (преобразования Лоренца – прим. наше) сводится к следующему: продольные – в направлении движения – размеры быстро движущегося тела сокращаются. Еще в 1909 году известный физик Пауль Эренфест усомнился в этом выводе. Вот его возражение: допустим, движущиеся предметы, действительно сокращаются. Хорошо, проведем опыт с диском. Будем вращать его, постепенно увеличивая скорость. Размеры диска, как говорит г-н Эйнштейн, будут уменьшаться; кроме того, диск искривится. Когда же скорость диска достигнет скорости света, диск попросту исчезнет. Эйнштейн оказался в шоке, потому, что Эренфест был прав ... а затем (Эйнштейн – прим. наше) помог оппоненту получить должность профессора физики ... В свою очередь, со страниц книг о частной теории относительности исчезает ... парадокс Эренфеста»
Итак, в рамках СТО пространство в движущихся системах отсчета реально сжимается, а время столь же реально замедляется. Если это так, пространственно-временные искажения должны отразиться и на процессах взаимодействий для всех без исключения явлений природы. И здесь сразу же возникли, так называемые, динамические парадоксы.
Рассмотрим парадокс рычага. Представим себе Г-образный рычаг, изображенный на рис.2. Этот рычаг уравновешен силами. Если мы теперь будем двигаться относительно этого рычага, то увидим (в полном соответствии со СТО), что длины плеч рычага и величины векторов сил изменились. Они изменились так, что возник вращающий момент, стремящийся повернуть этот рычаг. Повернется ли рычаг?
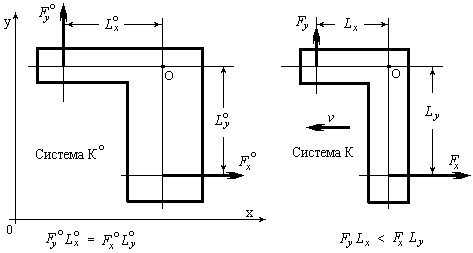
Рис. 2. Парадокс рычага
Мы не будем пересказывать беспомощное, противоречивое объяснение и давать ему критические замечания. Это сделано в Приложении 3 Части 6 работы [8]. Отметим лишь следующее. Как утверждают апологеты СТО, движущийся неуравновешенный рычаг вопреки законам механики не будет вращаться!
Зададим законные вопросы:
Предсказывая появление вращающего момента, действующего на движущийся рычаг, теория ошибается или же законы механики не «работают»?
Как можно определить: когда теория предсказывает правильный результат, которому можно доверять, а когда предсказываемый результат необходимо отбросить?