Курсовая работа: Обоснование организации связи в районе чрезвычайной ситуации

Эта таблица по написанию сходна с рядом распределения прерывной случайной величины X с возможными значениями x_1, x_2, …,x_n имеющими вероятности p₁ , p₂ ,…, p_n . И действительно, между системой X с конечным множеством состояний и прерывной случайной величиной много общего; для того чтобы свести первую ко второй, достаточно приписать каждому состоянию какое-то числовое значение (скажем, номер состояния). Для описания степени неопределенности системы совершенно неважно, какие именно значения x_1, x_2, …,x_n записаны в верхней строке таблицы; важны только количество этих значений и их вероятности.

В качестве меры априорной неопределенности системы (или прерывной случайной величины X) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

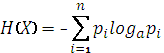(2.3)

Знак минус перед суммой поставлен для того, чтобы энтропия была положительной (числа р меньше единицы и их логарифмы отрицательны).

Энтропия H(X) обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие – невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний – увеличивается. Наконец, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.

Логарифм в формуле (2.3) может быть взят при любом основании а > 1. Перемена основания равносильна простому умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 – о «двоичных единицах». На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах; это хорошо согласуется с применяемой в цифровых каналах связи двоичной системой счисления.

Примем а = 2.

Легко убедиться, что при выборе 2 в качестве основания логарифмов за единицу измерения энтропии принимается энтропия простейшей системы X, которая имеет два равновозможных состояния:

x i	x1	x2
pi

По формуле (2.3) имеем

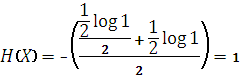
Определенная таким образом единица энтропии называется «двоичной единицей» и иногда обозначается bit (от англ. «binarydigit» – двоичный знак). Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.

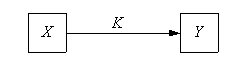????? ??????? ???????? ?????????? X ? ???????? Y, ????????? ??????? ????? ? (???. 2.4).

Рис. 2.4. Направление передачи информации

Известна производительность источника информации H₁ (X), т. е. среднее количество двоичных единиц информации, поступающее от источника в единицу времени (численно оно равно средней энтропии сообщения, производимого источником в единицу времени). Пусть, кроме того, известна пропускная способность канала С₁ , т.е. максимальное количество информации (нап