Курсовая работа: Определение мольной теплоемкости методом интерполяции
В нашем случае рассматриваются данные варианта №5.
№ варианта | |||
| 5 | 29.2752 | 33.5485 | 35.9109 |
4. Математические модели, применяемые для расчетов
Интерполяционный многочлен mср =f(t0 ), будет иметь следующий вид:
![]() ,
,
на основе него составляется система линейных уравнений, разрешив которую относительно коэффициентов a, b, d, получим интерполяционную функцию. Составим для этих данных интерполяционные уравнения:
1. 
![]()
2. ![]()
![]()
3. ![]()
![]()
4. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.![]()
![]()
![]()
y=29,2752+0,0104575*t-0,0000038218*t2
5. Результатырасчетов
| t°,C | mср | t°,C | mср |
| 0 | 29.2752 | 400 | 32.8467 |
| 10 | 29.3794 | 410 | 32.9203 |
| 20 | 29.4828 | 420 | 32.9932 |
| 30 | 29.5855 | 430 | 33.0653 |
| 40 | 29.6874 | 440 | 33.1366 |
| 50 | 29.7885 | 450 | 33.2072 |
| 60 | 29.8889 | 460 | 33.2770 |
| 70 | 29.9885 | 470 | 33.3460 |
| 80 | 30.0873 | 480 | 33.4143 |
| 90 | 30.1854 | 490 | 33.4818 |
| 100 | 30.2827 | 500 | 33.5485 |
| 110 | 30.3793 | 510 | 33.6145 |
| 120 | 30.4551 | 520 | 33.6797 |
| 130 | 30.5701 | 530 | 33.7441 |
| 140 | 30.6643 | 540 | 33.8078 |
| 150 | 30.7578 | 550 | 33.8707 |
| 160 | 30.8506 | 560 | 33.9329 |
| 170 | 30.9425 | 570 | 33.9943 |
| 180 | 31.0337 | 580 | 34.0549 |
| 190 | 31.1242 | 590 | 33.1148 |
| 200 | 31.2138 | 600 | 34.1739 |
| 210 | 31.3027 | 610 | 34.2322 |
| 220 | 31.3909 | 620 | 34.2897 |
| 230 | 31.4783 | 630 | 34.3466 |
| 240 | 31.5649 | 640 | 34.4026 |
| 250 | 31.6507 | 650 | 34.4579 |
| 260 | 31.7358 | 660 | 34.5124 |
| 270 | 31.8201 | 670 | 34.5661 |
| 280 | 31.9037 | 680 | 34.6191 |
| 290 | 31.9865 | 690 | 34.6713 |
| 300 | 32.0685 | 700 | 34.7228 |
| 310 | 32.1497 | 710 | 34.7735 |
| 320 | 32.2302 | 720 | 34.8234 |
| 330 | 32.3100 | 730 | 34.8725 |
| 340 | 32.3890 | 740 | 34.9209 |
| t°,C | mср | t°,C | mср |
| 750 | 34.9686 | 1150 | 36.2470 |
| 760 | 35.0154 | 1160 | 36.2633 |
| 770 | 35.0615 | 1170 | 36.2788 |
| 780 | 35.1069 | 1180 | 36.2936 |
| 790 | 35.1514 | 1190 | 36.3076 |
| 800 | 35.1952 | 1200 | 36.3208 |
| 810 | 35.2383 | 1210 | 36.3333 |
| 820 | 35.2806 | 1220 | 36.3450 |
| 830 | 35.3221 | 1230 | 36.3559 |
| 840 | 35.3628 | 1240 | 36.3661 |
| 850 | 35.4028 | 1250 | 36.3755 |
| 860 | 35.4420 | 1260 | 36.3842 |
| 870 | 35.4805 | 1270 | 36.3920 |
| 880 | 35.5185 | 1280 | 36.3992 |
| 890 | 35.5551 | 1290 | 36.4055 |
| 900 | 35.5913 | 1300 | 36.4111 |
| 910 | 35.6267 | 1310 | 36.4159 |
| 920 | 35.6613 | 1320 | 36.4200 |
| 930 | 35.6952 | 1330 | 36.4233 |
| 940 | 35.7283 | 1340 | 36.4258 |
| 950 | 35.7607 | 1350 | 36.4276 |
| 960 | 35.7922 | 1360 | 36.4286 |
| 970 | 35.8230 | 1370 | 36.4288 |
| 980 | 35.8531 | 1380 | 36.4283 |
| 990 | 35.8824 | 1390 | 36.4270 |
| 1000 | 35.9109 | 1400 | 36.4250 |
| 1010 | 35.9387 | 1410 | 36.4222 |
| 1020 | 35.9656 | 1420 | 36.4186 |
| 1030 | 35.9919 | 1430 | 36.4142 |
| 1040 | 36.0173 | 1440 | 36.4091 |
| 1050 | 36.0420 | 1450 | 36.4032 |
| 1060 | 36.0660 | 1460 | 36.3966 |
| 1070 | 36.0891 | 1470 | 36.3892 |
| 1080 | 36.1116 | 1480 | 36.3810 |
| 1090 | 36.1332 | 1490 | 36.3721 |
| 1100 | 36.1541 | 1500 | 36.3624 |
| 1110 | 36.1742 | ||
| 1120 | 36.1935 | ||
| 1130 | 36.2121 | ||
| 1140 | 36.2299 |
График:
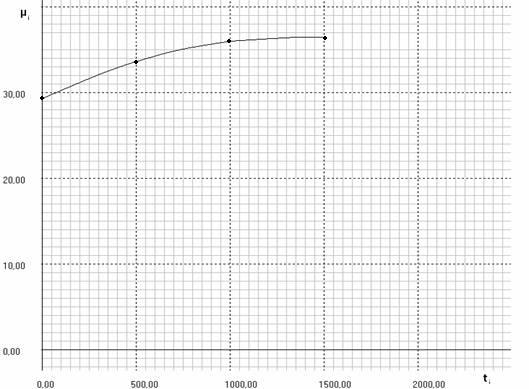
6. Текст программы
#include<stdio.h>
#include<conio.h>
#include<math.h>
float andrey (float c1, float c2, float m);
void main()
{clrscr();
float p1,p2,b,d;
int t1=500,i;
float k1=29.2752,k2=33.5485,k3=35.9109;