Курсовая работа: Оптическая изомерия
Если среда ахиральна, две циркулярнополяризованные составляющие проходят с одинаковой скоростью (т.е. с одинаковыми показателями преломления для правого и левого лучей). Однако хиральные молекулы проявляют анизотропию поляризуемости, которая зависит от того, левую или правую спиральность имеет циркулярнополяризованный луч. При прохождении через хиральную среду в общем случае неодинаковы не только скорости, но и коэффициенты поглощения левого и правого циркулярнополяризованных компонент плоскополяризованного света. В результате векторы для правого и левого прошедшего через образец лучей будут иметь разную амплитуду, а результирующий вектор будет описывать эллиптическую траекторию. В общем, при прохождении плоскополяризованного света через хиральную среду вектор электрического поля начинает описывать эллипс (эллиптическая поляризация) с повернутой главной осью.
Угол вращения уменьшается с увеличением длины волны падающего света. Однако это справедливо лишь для света, длина волны которого больше длины волны максимума поглощения в электронном спектре данного вещества. Изменение оптического вращения при изменении длины волны называется дисперсией оптического вращения (ДОВ). Разность поглощения правой и левой компонент называется круговым дихроизмом (КД). Количественной характеристикой КД служит угол эллиптичности y, величина которого обратно пропорциональна длине волны
КД открыт Э. Коттоном в 1911 г. и его часто называют эффектом Коттона. ДОВ и КД вместе называются хирооптическими явлениями; в своей основе они связаны с электронными переходами в хиральном окружении. Эффект Коттона, т.е. превращение плоскополяризованного света в эллиптически поляризованный заметно проявляется главным образом вблизи полос собственного (резонансного) поглощения вещества.
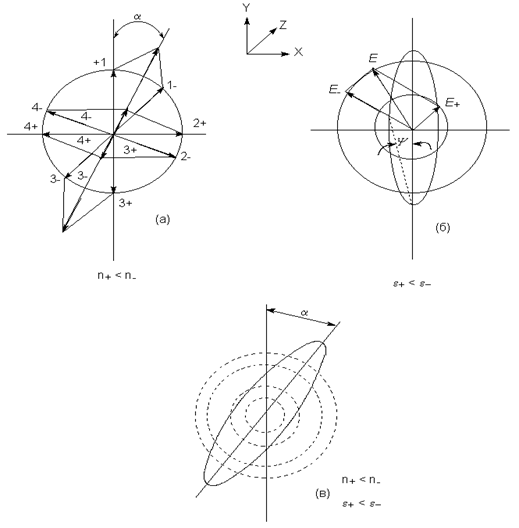
(а) - Взаимодействие сдвинутых по фазе компонентов равной амплитуды, (б) - взаимодействие находящихся в фазе компонентов разной амплитуды, (в) - суммарный результат сдвига по фазе.
1.2 б. Квантовая теория
Квантовую теорию оптической активности построил в 1928 г. бельгийский физик Л. Розенфельд. С позиций современной науки эта теория рассматривается как более строгая. Для объяснения оптической активности оказалось необходимым учитывать взаимодействие электрических и магнитных дипольных моментов, наведенных в молекуле полем проходящей световой волны.
1.2 в. Корпускулярная теория
В настоящее время возрождается интерес к корпускулярной теории света, которой придерживался еще Ньютон. Частицей света является фотон - реальная элементарная частица. В фотонной теории поляризацию света связывают с поляризацией фотонов, которая обусловлена наличием у этих частиц спина и его определенной направленностью в пространстве. Спиновые квантовые числа - это как бы дополнительные внутренние степени свободы частицы. В отличие от электронов, имеющих спин J = 1/2, спин фотона J = 1. (Это означает, что электроны принадлежат к классу фермионов, для которых справедлив запрет Паули, а фотоны - к классу бозонов, для которых не действует принцип запрета). Согласно квантовой механике, частица со спином J и ненулевой массой покоя имеет (2J + 1) внутренних квантовых состояний, определяющих ее поляризацию, т.е. степень асимметрии частицы в пространстве. Но масса покоя фотона равна нулю, и поэтому число спиновых состояний на единицу меньше, т.е. равно двум (+1 и - 1). Это означает, что возможны лишь две ориентации проекции спина фотона на направление его движения: параллельная и антипараллельная. В таком случае возникает понятие "спиральность частицы". Если проекция спина на направление движения положительна, то говорят, что частица имеет правовинтовую (правую) спиральность, а если отрицательна - левовинтовую (левую) спиральность. Спиральные объекты хиральны, поэтому фотоны являются как бы хиральными частицами.
Поскольку фотоны обладают целочисленным спином, в одном и том же состоянии может находится любое число фотонов. Это обусловливает возможность описания электромагнитных взаимодействий с участием большого числа фотонов в рамках классической (а не только квантовой) механики. Циркулярно-поляризованный свет можно рассматривать как поток фотонов, имеющих только правую или только левую спиральность. Плоскополяризованный свет состоит из одинакового количества "левых" и "правых" фотонов. Взаимодействие по-разному поляризованных фотонов с хиральной анизотропной средой происходит неодинаково, что приводит к хироптическим эффектам.
Ахиральная молекула не вращает плоскость поляризации света только при определенной ее ориентации по отношению к падающему лучу. Например, ахиральная молекула, имеющая плоскость симметрии, не вращает плоскость поляризации лишь в том случае, если плоскость поляризации совпадает с плоскостью симметрии. Все же остальные молекулы, не ориентированные таким образом, вращают плоскость поляризации, даже не будучи хиральными. Однако в целом образец не вращает, так как в массе молекулы ориентированы беспорядочно, и одни молекулы вращают плоскость поляризации в одном направлении, а другие молекулы, встречающиеся на пути светового луча, вращают ее в противоположную сторону. Таким образом коллектив ахиральных молекул имеет суммарное вращение, равное нулю, хотя каждая молекула может вращать плоскость поляризации. В случае хиральных соединений молекул противоположной ориентации (если это не рацемическая смесь) просто не может существовать, и вращение наблюдается.
2. Хиральные молекулы
В случае простых молекул легко проводится зрительное распознавание несовместимости с зеркальным отображением. Однако многие органические молекулы настолько сложны, что такой способ требует очень развитого пространственного воображения, которым обладают далеко не все.
2.1 Точечные группы симметрии
Шар самый симметричный объект, его не возможно отразить в зеркале. Он всегда выглядит одинаково. Тетраэдр "менее симметричен", чем шар, поскольку вокруг высоты его нужно повернуть лишь на определенный угол (1200), чтобы он выглядел так же, как до поворота. Вращение вокруг оси является одной из операций симметрии. Операцией симметрии называется действие над объектом, которое приводит к его новой ориентации, неотличимой от исходной и совмещаемой с нею.
Каждой операции симметрии соответствует определенный элемент симметрии. Элементом симметрии называется геометрическое место точек, остающихся неподвижными при данной операции симметрии. Основными элементами симметрии являются собственные оси вращения, которые в системе обозначений Шенфлиса имеют символ Cn, где n - порядок оси, означающий, что поворот молекулы на угол 2p /n радиан приводит к структуре, неотличимой от первоначальной, несобственные оси вращения или зеркально-поворотные оси (s n), зеркальные плоскости симметрии (s), делящие молекулу пополам, так, что одна половина является зеркально-симметричной другой половине, центр инверсии (i) и тождественное преобразование (Е). В соответствии с этим операции симметрии делят на поворот оси вокруг оси симметрии Сn, поворот вокруг оси с последующим отражением в плоскости, перпендикулярной этой оси (Sn), отражение в плоскости симметрии s, инверсию в центре симметрии i и операцию идентичности Е. При операции идентичности с молекулой ничего не делают, но эта операция не бессмысленна, т.к. она позволяет включить в единую классификацию как симметричные, так и асимметричные объекты.
2.1 а. Собственная ось симметрии
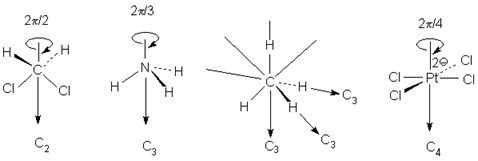
Все молекулы имеют тривиальную ось С1, поскольку в любом случае вращение на 3600 возвращает молекулу в исходное состояние. Следовательно, операция С1 эквивалентна операции идентичности (С1 є Е). Дихлорметан имеет ось С2, аммиак - ось С3, метан - четыре оси С3, тетрахлорплатинат - ось С4.
2.1 б. Несобственная ось симметрии
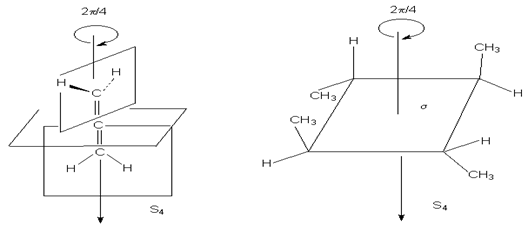
Простейшая зеркально поворотная ось S1 эквивалентна перпендикулярной ей плоскости симметрии (S1 є s). Примером является молекула хлорфторметана. Зеркально-поворотные оси более высокого порядка (Sn) можно рассматривать как комбинацию вращения на угол 2p /n с последующим отражением в плоскости, перпендикулярной оси вращения. Так, аллен и изображенный ниже изомер 1,2,3,4-тетраметилциклобутана имеет зеркально-поворотную ось S4:
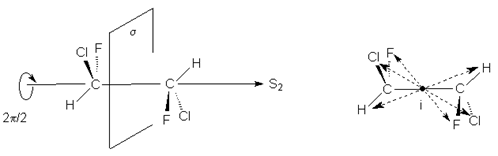
1,2-Дихлор-1,2-дифторэтан обладает осью S2, которая совпадает со связью С-С. Операция S2 эквивалентна инверсии в центр симметрии, который находится посредине связи С-С (S2 є i)
Поскольку у молекул может быть не один, а несколько элементов симметрии, их удобнее классифицировать по точечной группе симметрии. Набор все операций симметрии объекта образует его группу симметрии. Если при всех этих преобразованиях остается неподвижным центр тяжести фигуры, то группа симметрии называется точечной. Известны четыре типа точечных групп симметрии.
2.1 в. Типы точечных групп симметрии
К типу 1 относятся точечные группы С1, Сs, Ci, которые не имеют нетривиальных поворотных осей, поэтому их называют неаксиальными. К типу 2 относятся группы с единственной поворотной осью. В группе Cn других элементов симметрии нет, в группе Cnv имеется n вертикальных плоскостей s n, проходящих через ось Cn, а в группе Сnh одна горизонтальная плоскость s h, перпендикулярная оси Сn. Сюда же входит группа Sn, поскольку при наличии зеркально-поворотной оси порядка n обязательно имеется и собственная ось порядка n/2 (C2 у S4, C3 у S6 и т.д.). При нечетном n оси Sn могут быть представлены как комбинации других операций. Для низших порядков S1 є s и S2 є i. Точечные группы типа 3 имеют одну ось Сn и n осей второго порядка, перпендикулярных оси Сn. Такие группы называются диэдральными. Если нет плоскостей симметрии, группа обозначается как Dn, если имеется несколько плоскостей s v (вертикальных) - Dnd, а если еще и горизонтальная плоскость s h, то группа обозначается Dnh. К типу 4 относятся точечные группы, имеющие более чем одну ось порядка выше двух. Такие группы называются кубическими. К ним относятся точечные группы правильных тетраэдра (Td), октаэдра и куба (Oh), икосаэдра и додекаэдра (Ih). Максимальную симметрию имеет шар, который принадлежит предельной группе Kh, включающей все возможные операции симметрии.
2.2 Симметричное определение хиральности
Хиральна любая истинно асимметрическая молекула, относящаяся к группе С1, не имеющая никаких элементов симметрии, кроме идентичности (и оси С1, т.к. С1 ![]() Е). Очевидно, также, что молекулы, имеющие плоскость симметрии (s) или центр симметрии (i) ахиральны, поскольку они состоят из двух одинаковых "половинок" и в зеркальном отображении левая и правая половинки преобразуются друг в друга или без поворотов (при наличии плоскости), или с поворотом на 1800 (при наличии центра инверсии). Молекулы, имеющие зеркально-поворотные оси (Sn) также совмещаются со своим зеркальным отображением, и поэтому ахиральны. Следовательно, хиральны только молекулы, относящиеся к аксиальным точечным группам Сn и Dn.
Е). Очевидно, также, что молекулы, имеющие плоскость симметрии (s) или центр симметрии (i) ахиральны, поскольку они состоят из двух одинаковых "половинок" и в зеркальном отображении левая и правая половинки преобразуются друг в друга или без поворотов (при наличии плоскости), или с поворотом на 1800 (при наличии центра инверсии). Молекулы, имеющие зеркально-поворотные оси (Sn) также совмещаются со своим зеркальным отображением, и поэтому ахиральны. Следовательно, хиральны только молекулы, относящиеся к аксиальным точечным группам Сn и Dn.
Таким образом, можно сформулировать симметрийный критерий хиральности: любая молекула, которая не имеет несобственной оси вращения Sn хиральна.
Впервые доказательство справедливости данного определения хиральных молекул получено при исследовании изомерных четвертичных аммонийных солей со спирановым атомом азота IV, V, VII и IX. Изомеры IV и V асимметричны (группа C1), изомер VII диссимметричен (группа D2). Поэтому эти три изомера должны быть хиральными. И действительно, они были получены в оптически активной форме. Однако изомер VIII относится к группе S4, т.е. ахирален, и получить его в оптически активной форме нельзя.
2.3 Типы хиральности
Молекулы, содержащие тетраэдрический атом, например, углерода с четырьмя разными заместителями принадлежат к точечной группе С1. Они асимметричны и центральный атом называется асимметрическим атомом.
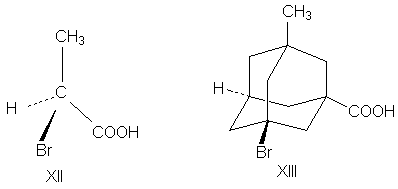
Адамантаны, у третичных атомов углерода которых имеется четыре разных заместителя, хиральны и оптически активны. При сравнении формул симметрия обоих соединений очень похожа. Остов адамантана можно представить как тетраэдр с "изломанными ребрами", он имеет симметрию Td которая переходит в C1, когда все четыре заместителя у третичных атомов углерода разные. У производного адамантана нет асимметрического атома углерода, как в a-бромпропионовой кислоте, но есть центр, находящийся внутри молекулы (центр тяжести незамещенного адамантана).
Асимметрический центр - это частный случай более общего понятия хиральный центр. Хиральный центр может иметь не только асимметрические молекулы, но и молекулы симметрии Cn или Dn. Хиральный центр является лишь одним из возможных элементов хиральности. Однако кроме центрального существуют еще и аксиальный, планарный и спиральный типы хиральности.
Аксиальной хиральностью обладают молекулы, имеющие хиральную ось. Хиральную ось легко получить, мысленно "растягивая" центр хиральности: