• ввести ключевое слово Given ;

• ввести систему ограничений с использованием жирного знака равенства, нажав комбинацию клавиш Ctrl+= ;

• ввести граничные значения;

• ввести вектор-столбец искомых параметров, используя диалоговое окно Insert Matrix (Вставить матрицу) и комбинацию Ctrl+M . В диалоговом окне число строк (Rows) – элементов вектора столбца – должно быть равно 7, а число столбцов (Columns) – 1;

• ввести знак присваивания, нажав комбинацию клавиш Shift+: (двоеточие);

• ввести функцию Maximize с искомыми параметрами, используя диалоговое окно Insert Function (Вставить функцию) и комбинацию Ctrl+E ;

• ввести вектор-столбец искомых параметров и знак ``равно''.

На рис. 1 показан процесс оптимизации распределения неоднородных ресурсов с помощью Mathcad.

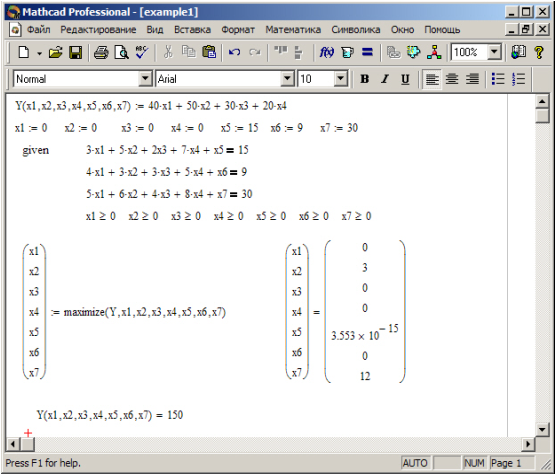
Решение задачи А с помощью Mathcad

Оптимальное распределение неоднородных ресурсов зафиксировано в векторе . Из полученного решения видно, что , , , , , . Это означает, что изделия , и предприятие изготавливать не должно. Ему нужно производить только второе изделие в количестве 3 единиц. Цифра в переменной определяет изделие, планируемое для изготовления. Оптимальное распределение ресурсов обеспечит получение максимальной прибыли , которая составит 150 единиц.

В качестве еще одного примера решим в системе Mathcad следующую задачу линейного программирования:

Приведем ее к каноническому виду:

(6)

Очевидно, что в качестве начального приблежения необходимо взять Решение задачи приведено на рисунке 2.

Решение задачи (6) с помощью Mathcad pic2

Задача о нахождении минимума целевой функции, в системе символьной алгебры Mathcad, решается так же просто. Для этого достаточно заменить функцию maximize на minimize .

Как показывает практика Mathcad корректно решает задачи в которых функция не достгает максимума (минимума) на ограниченном множестве. В этом случае Mathcad выводит соответствующее сообщение (см. рис. 3).

Решение задачи не имеющей максимума pic3

К сожалению Mathcad некорректно решает задачи в которых оптимальное решение неединственно. В этом случае решением служит одна из точек в которых достигается максимум (минимум). Так например при решении задачи (6) симплекс-методом, то получим, что . В обоих случаях . Лучше всего это прослеживается при решении следующей задачи:

(7)

Очевидно, что , а

Задавая начальные приближения в соответствии с формулой приведенной выше, Mathcad будет выдавать в качестве ответа начальные приближения.

В случае задачи (7) нам действительно безразлично в каком количестве выпускать товары 1 и 2, прибыль от этого не меняется. Но если мы откажемся от выпуска одного из товаров, мы повысим прибыль за счет снижения затрат на обслуживание одного из станков, мы можем его вообще продать, сдать в аренду, сократить рабочих, обслуживающих данный станок. Решение в таком случае должен принимать управляющий.

Заключение

Как было показано выше система символьной математики идеально подходит для решения задач исследования операций и в частности задач оптимального распределения неоднородных ресурсов. Mathcad в считаные секунды находит решение подобных задач, даже в случае порядка ста или двухсот переменных.

Приведенным алгоритмом можно пользоваться и в случае, если задача представляет собой задачу выпуклого программирования с нелинейными ограничениями и с нелинейной целевой функцией.