Курсовая работа: Основы расчёта оболочек

Условие задачи: Построить эпюры безмоментных напряжений и для сферического сосуда (рис. 1), полностью заполненного жидкостью.

Исходные данные:

Радиус оболочки: м;

Плотность жидкости (окислитель):

;

Толщина стенки оболочки:

.

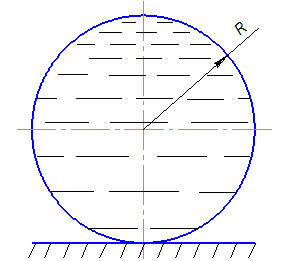
Рис. 1. Схема оболочки

Выполнение расчёта

1. Выводы расчётных зависимостей для верхней полусферы

В верхней полусфере отсечём часть оболочки нормальным коническим сечением с углом при вершине конуса и составим уравнение равновесия отсеченной части оболочки (рис. 2):

,

где – равнодействующая сил давления жидкости на стенку оболочки в проекции на

вертикальную ось.

Жидкость действует на стенку оболочки переменным давлением. Равнодействующую сил давления жидкости на вертикальную ось определим по формуле:

,

где – объём цилиндра; – объём шарового сегмента, рис. 2.

,

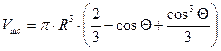где - высота столба жидкости в расчётном сечении.

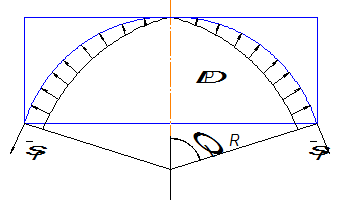
Рис. 2. Расчётная схема

Получаем:

.

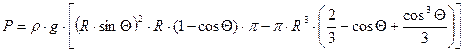Из уравнения равновесия после подстановки выражения для силы имеем:

.

Отсюда меридиональное напряжение:

.