Курсовая работа: Основы расчёта оболочек
Погонный изгибающий момент по длине оболочки 
с учётом податливости шпангоута:
Результаты вычислений заносим в таблицу 1 и строим график функции 
, совмещённый с графиком 
(рис.2, рис.3).
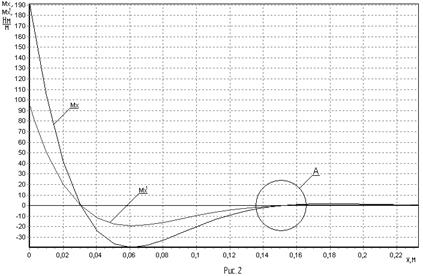
Определим в процентах снижение величины изгибающего момента 
при учёте податливости шпангоута:
;
Таблица 1
2. ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПОЛУСФЕРИЧЕСКОЙ ОБОЛОЧКИ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ
Условие задачи: Тонкостенный сосуд (рис.1), выполненный в виде полусферы, частично заполнен жидкостью. Закрепление оболочки по диаметру окружности – свободное.
Цель расчета:
1. Построить эпюры погонных меридиональных 
и кольцевых 
усилий.
2. Определить толщину стенки оболочки, без учёта её собственного веса.
Исходные данные:
Радиус сферы: 
м;
Угол зеркала жидкости: 
;
Плотность жидкости (горючее):
;
Коэффициент безопасности 
;
Материал оболочки:
Марка ВТ6С (О);
предел прочности 
.
Выполнение расчёта
1. Расчёт участка оболочки над уровнем жидкости
Рассмотрим участок оболочки 
(рис. 1). На расстоянии 
от полюса 
отсекаем часть оболочки нормальным коническим сечением с углом широты 
(рис. 2).