Курсовая работа: Оцінка ефективності використання рухомого складу

Середня арифметична зважена. Оскільки сукупність згрупована, а частоти варіантів задані явно, то визначаємо середню арифметичну зважену величину:

;

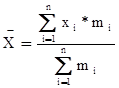де Х_і – індивідуальні значення ознаки;

m_і ‑ кількість однакових варіант.

Структурні середні характеризують структуру варіаціонних рядів. До них відносяться мода і медіана. Вони виражають визначене значення ознаки у ряду розподілу.

Мода – значення ознаки, що найбільш часто повторюється.

Медіаною називається значення ознаки, що знаходиться в середині ранжируємого ряду і поділяє цей ряд на дві рівні частини

Структурні середні

а) визначення моди:

;

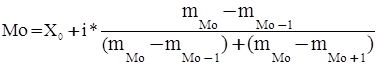де Х₀ – нижня границя модального інтервалу;

і – величина інтервалу;

m_Mo ‑ відносна частота модального інтервалу;

m_Mo-1 ‑ відносна частота, передуючого модальному, інтервалу;

m_Mo+1 – відносна частота, наступного після модального, інтервалу.

б) визначення медіани:

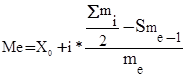
де Х₀ – нижня границя медіанного інтервалу;

і – величина інтервалу;

m_і – загальна сума частот усіх інтервалів;

m_е – частота медіанного інтервалу;

Sm_e-1 – сума частот до медіанного інтервалу.

Крім визначення середніх величин в цьому пункті курсової роботи знаходимо показники варіації. Вони показують коливність ознаки у сукупності. До них відносяться: розмах варіації, середньо лінійні відхилення, середньоквадратичні відхилення і дисперсія

Показники варіації:

а) середньоквадратичне відхилення - показує наскільки в середньому індивідуальне значення відхиляється від середнього, але з врахуванням знаку.

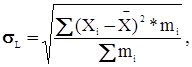
б) дисперсія

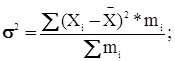
Відносні показники варіації(коефіцієнти варіації):