Курсовая работа: Параметричні і непараметричні критерії для перевірки гіпотез
1. Відомості про деякі відомі розподіли
Дискретна випадкова величина (біноміальний розподіл) описується схемою Бернуллі: якщо випадкова подія А в n незалежних іспитах зустрілася m разів, то р – імовірність появи події А у кожному іспиті. Формула Бернуллі (дозволяє оцінити імовірність того, що серед n взятих навмання елементів виявиться m очікуваних. Даний розподіл характеризується двома параметрами: середнім числом очікуваного результату ![]() (математичне очікування) і дисперсією частоти події А в n незалежних іспитах
(математичне очікування) і дисперсією частоти події А в n незалежних іспитах
![]()
і має вигляд

Граничним випадком біноміального розподілу є формула Пуассона:

Випадкова величина розподілена за законом Пуассона, якщо вона приймає рахункову множину можливих значень 0, 1, 2, з імовірностями ![]() . Коли у схемі Бернуллі імовірність появи події А (величина p = соті чи тисячні частини одиниці), тобто частина успіхів дуже мала, розподіл частот таких рідких подій у n іспитах стає несиметричним і зазвичай описується формулою Пуассона. Розподіл характеризується одним параметром – середньою величиною, рівною a, середнє квадратичне відхилення в даному випадку також дорівнює а. Для такого розподілу характерна висока варіація. Зі зростанням значень а розподіл прагне до нормального закону. Розподіл Пуассона є моделлю, яку можна використовувати для опису випадкового числа появи визначених подій у фіксованому проміжку часу.
. Коли у схемі Бернуллі імовірність появи події А (величина p = соті чи тисячні частини одиниці), тобто частина успіхів дуже мала, розподіл частот таких рідких подій у n іспитах стає несиметричним і зазвичай описується формулою Пуассона. Розподіл характеризується одним параметром – середньою величиною, рівною a, середнє квадратичне відхилення в даному випадку також дорівнює а. Для такого розподілу характерна висока варіація. Зі зростанням значень а розподіл прагне до нормального закону. Розподіл Пуассона є моделлю, яку можна використовувати для опису випадкового числа появи визначених подій у фіксованому проміжку часу.
Безперервний розподіл – це рівномірний розподіл на відрізку [0,1]:
![]()
Безперервний розподіл можна розповсюджувати на випадок відрізка [0,1], тоді імовірність приймати значення в будь-якій точці відрізка дорівнює ![]() . Математичне очікування розподілу дорівнює
. Математичне очікування розподілу дорівнює ![]() , дисперсія дорівнює
, дисперсія дорівнює ![]() .
.
Безперервний експонентний (показовий) розподіл має вигляд:
![]()
де ![]() – параметр експонентного розподілу.
– параметр експонентного розподілу.
Математичне очікування дорівнює ![]() , а дисперсія –
, а дисперсія – ![]() .
.
5. Розподіл Максвелла (безперервний розподіл) має вигляд:
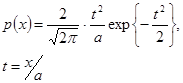
і описує асиметричні розподіли. У цій формулі параметр а дорівнює середньому арифметичному, помноженому на величину 0,6267. Характерною ознакою розподілу Максвелла є рівність середнього квадратичного відхилення величини 0,674а. Крива розподілу за формулою нагадує нормальний розподіл, але починається від нуля, крутіше піднімається з боку малих значень випадкової величини і потім, досягши максимуму, більш полого спадає убік великих значень. Такий розподіл виникає, наприклад, при побудові розподілу осіб і популяції за їхніми відстанями до оптимального фенотипу, що зворотньопропорційні їх фенотиповій цінності.
Розподіл Шарльє (безперервний) має вигляд:
![]()
де р(x) – щільність нормального розподілу;
р¢(x) – похідна відповідного порядку щільності нормального
розподілу р(х);
Ах – асиметрія;
Ех – ексцес.
Розподіл Шарльє описує асиметричний розподіл з вираженим ексцесом, що виникає при порушенні форми кривої, характерної для нормального розподілу. Така крива розподілу є асиметричною, її звоноподібна вершина стає пікоподібною, чи трапецієподібною. За допомогою розподілу такого виду «конструюються» порушення нормальної форми розподілу.
Гамма-розподіл (безперервний) має вигляд:
![]()
де Г(a) – гамма-функція. Її визначення за Ейлером задається співвідношенням:
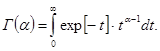
--> ЧИТАТЬ ПОЛНОСТЬЮ <--