Курсовая работа: Полупроводниковые наноструктуры

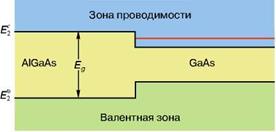
Рис. 1 - Энергетические зоны на границе двух полупроводников - гетероструктуре. и - границы зоны проводимости и валентной зоны, E_g - ширина запрещенной зоны. Электрон с энергией меньше (уровень показан красным цветом) может находиться только справа от границы

Когда движение электрона происходит в ограниченной области, его энергия имеет строго определенные, дискретные значения. Говорят, что спектр энергий квантован.

В квантовой механике электрон не бегает в ограниченной области, как классическая частица. Если он заперт в атоме, молекуле или любой потенциальной яме, то волновая функция Ч представляет стоячую волну. Если речь идет о прямоугольной потенциальной яме, которая изображена на рис. 2, то по своей форме волна будет такой же, как и в случае натянутой струны, но дискретным в этом случае будет не спектр частот, а спектр энергий. Стоячие волны, описывающие электронные состояния в яме, – это синусоиды, обращающиеся в точках x = 0 и x = a в нуль.

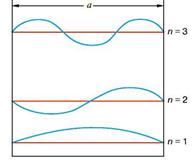
Рис. 2 - Волновые функции и уровни энергии частицы, находящейся в бесконечно глубокой потенциальной яме. Показаны три нижних энергетических уровня (красный цвет) и три волновые функции

,(1)

где n– номер квантового состояния, a – размер ямы. На рис. 2 изображены три такие функции, соответствующие n = 1, 2, 3, … Электронная плотность в яме распределяется неравномерно, есть максимумы и минимумы плотности вероятности. Из формулы (1) следует также, что длины волн Ч'-функций, описывающих электронные состояния с различными n, удовлетворяют условиям , то есть в яме укладывается целое число полуволн.

1.2 Особенности энергетических уровней

Найдем разрешенные уровни энергии электрона, находящегося в потенциальной яме. Воспользуемся правилом квантования Н. Бора. Согласно постулату Бора, в потенциальной яме разрешены лишь те траектории, для которых импульс частицы p_n и ширина ямы a связаны соотношением (2)

Здесь n – номер квантового состояния. Определив отсюда разрешенные значения импульса, найдем и уровни энергии в яме:

(3)

Минимальная энергия частицы, находящейся в яме, не может быть равной нулю. Всегда существует так называемая энергия нулевых колебаний, которая, согласно формуле (3), равна n² h² /(2ma² ). Вычислим, какой порядок имеет величина первого уровня в реальной квантовой яме. Если ширина ямы равна 5 нм, то, согласно (3), имеем E₁ = 0,02 эВ. Нужно, однако, иметь в виду, что электронная масса в кристалле может существенно отличаться от массы свободного электрона m = 10^-27 г. В типичной ситуации эффективная масса в квантовой яме в десять раз меньше массы свободного электрона. Тогда при той же ширине ямы получим E₁ = 0,2 эВ. Эта величина и определяет характерный масштаб электронных энергий в квантовых структурах.

1.3 Применение квантовых наноструктур в электронике

Рассмотрим принцип действия двух основных приборов современной квантовой электроники.

Резонансный туннельный диод.

В классической физике если полная энергия частицы меньше потенциальной энергии в области барьера, то эта частица отражается и затем движется в обратном направлении. В том случае, когда полная энергия превышает потенциальную, барьер будет преодолен. Квантовая частица ведет себя иначе: она преодолевает барьер подобно волне. Даже если полная энергия меньше потенциальной, есть вероятность преодолеть барьер. Это квантовое явление получило название "туннельный эффект". Оно используется в резонансном туннельном диоде.

Он состоит из двух барьеров, разделенных областью с малой потенциальной энергией. Область между барьерами – это как бы потенциальная яма, в которой есть один или несколько дискретных уровней. Характерная ширина барьеров и расстояние между ними составляют несколько нанометров. Области слева и справа от двойного барьера играют роль резервуаров электронов проводимости, к которым примыкают контакты. Электроны занимают здесь довольно узкий энергетический интервал. В приборе используется следующая особенность двойного барьера: его туннельная прозрачность имеет ярко выраженный резонансный характер. В том случае, когда энергия электронов, налетающих на барьеры, равна энергии дискретного уровня, туннельная прозрачность резко возрастает. При резонансе из-за интерференции волн во внутренней области гасится волна, отражающаяся от двойного барьера. Следовательно, волна, упавшая слева, полностью проходит направо.

Рассмотрим, как работает резонансный диод. Ток, протекающий через двойной барьер, зависит от величины приложенного напряжения. Потенциал в приборе падает главным образом в области двойного барьера, так как области слева и справа от него обладают высокой проводимостью. Если приложенное напряжение мало и энергия электронов, налетающих на барьер слева, меньше энергии дискретного уровня, то прозрачность барьера и, следовательно, протекающий ток будут малы. Ток достигает максимального значения при таких напряжениях, когда энергия электронов равна энергии дискретного уровня. При более высоких напряжениях энергия налетающих электронов станет больше энергии дискретного уровня и туннельная прозрачность барьера уменьшится. При этом ток также уменьшится. На вольт-амперной характеристике будет участок отрицательного дифференциального сопротивления. Благодаря этому в электронных схемах резонансный диод может использоваться не только как выпрямитель, но и выполнять самые разнообразные функции. Если к центральной области резонансного диода подвести контакт, через который можно управлять положением дискретного уровня, получится новый прибор – транзистор.

Резонансный туннельный диод – это первое реальное устройство с квантовой ямой и барьерами. Он был создан Лео Эсаки и Чангом в 1974 году. Идею прибора предложил Л. Иогансен еще в 1963 году.

Лазеры на квантовых ямах.

Квантовые структуры используются для создания лазеров. Уже сегодня эффективные лазерные устройства на квантовых ямах дошли до рынка и применяются в волоконно-оптических линиях связи. Для работы любого лазера необходимо создать инверсную населенность энергетических уровней. То есть, на более высоком уровне должнонаходиться больше электронов, чем на низком, в то время как в состоянии теплового равновесия ситуация обратная. Каждому лазеру необходим оптический резонатор или система зеркал, которая запирает электромагнитное излучение в рабочем объеме.

Для того чтобы квантовую яму превратить в лазер, нужно ее подсоединить к двум контактам, через которые электроны могут непрерывно поступать в рабочую область. Пусть через один контакт электроны поступают в зону проводимости. Далее, совершая скачки из зоны проводимости в валентную зону, они будут излучать кванты, то есть порции электромагнитного излучения (рис. 3). Затем через валентную зону носители тока должны уходить на другой контакт.

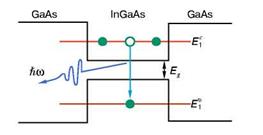
Рис. 3 - Энергетическая схема лазера на квантовой яме другой контакт

Частота излучения определяется условием (4),

где и – энергии первых энергетических уровней соответственно в зоне проводимости и валентной зоне, E_g – ширина запрещенной зоны.

Электромагнитное излучение, генерируемое лазером, нужно сконцентрировать в центральной, рабочей области прибора. Для этого показатель преломления внутренних слоев должен быть больше, чем внешних. Внутренняя область играет роль волновода. На границах этого волновода нанесены зеркала, которые образуют резонатор.