Курсовая работа: Построение ОВС для решения формулы

Для сорок второго варианта V=42=1010102, причём следует учесть, что направления движения чисел читаются с право налево, т.е. V=10 10 102, и 00-это юг, 01-запад, 10-север, 11-восток. С В А

Устройство должно выполнить вычисление за минимальное время, т.е. за минимальное количество тактов. Частично этого можно достичь, сократив время программирования ОЭ.

Т£ (X+Y+Z+6) ×16 (1.2.5)

При К=42, накладывается следующее ограничение тактов программирования:

T£ (9+0+0+6) ×16=15×16= 240.

Из предыдущих вычислений следует, что С вычисляется по формуле С=7|A-B|/4, число А двоично-пятиричное и поступает с севера, В - двоично-девятиричное и так же поступает с севера, вычитание производится в дополнительном коде, результат выдаётся на север и количество тактов программирования не превышает двухсот сорока.

2. Структура вычислительного процесса алгоритмы вычислений

2.1 Структура вычислительного процесса

? ??? ?????????? ????? ????????????? ?? ??? ???????????????, ??? ? ???????????. ? ?????????? ????? ?????????????? ??? ???????. ??????? ??? ??????????? ???????????? ????????? ???? ?? ???.1 ????????? ????????? ??????????????? ????????.

Рис.1.

2.2 Последовательность обработки операндов

2.2.1 Обработка числа А

Обработка числа заключается в том, что необходимо число перевести из двоично-кодированного вида в двоичный, а так же преобразовать его в дополнительный код, В таком виде оно пригодно для дальнейшего использования.

В начальных условиях указано, что операнд А можно считать положительным числом, а это означает, что прямой код числа совпадает с дополнительным.

Таким образом, обработка числа А состоит в выделении старшей тетрады, выделении младшей тетрады, умножении H на пять и сложении с L. Подробно эти действия представляет алгоритм на рис.2.

Число А2-5 поступает с севера. Выделение старшей тетрады производится путём логического умножения А 2-5 на константу вида 111100002 или F016. Это наглядно иллюстрирует пример:

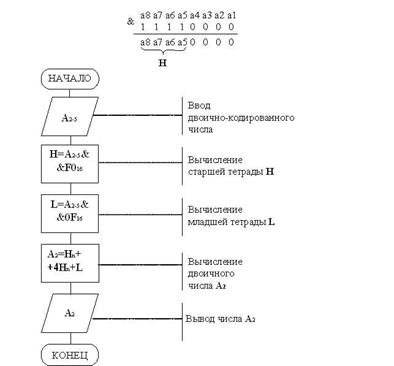
Рис.2

Младшая тетрада выделяется аналогичным способом:

Двоичное число находится по формуле (2.2.1 1)

A 2= Hn ×S + L ( 2.2.1 1)

где S -система счисления двоично-кодированного числа, L -его младшая тетрада, а Hn -нормализированная старшая тетрада двоично-кодированного числа:

а8 а7 а6 а5 0 0 0 0=H

0 0 0 0 а8 а7 а6 а5=Hn

Для сорок второго варианта формула (2.2.1 1) выглядит следующим образом: А2=5 ×Hn + L

Процедура умножения старшей тетрады на пять может быть представленной в виде: 5 Hn = Hn +4 Hn

2.2.2 Обработка числа В

Операнд В обрабатывается аналогично операнду А, за исключением некоторых особенностей.

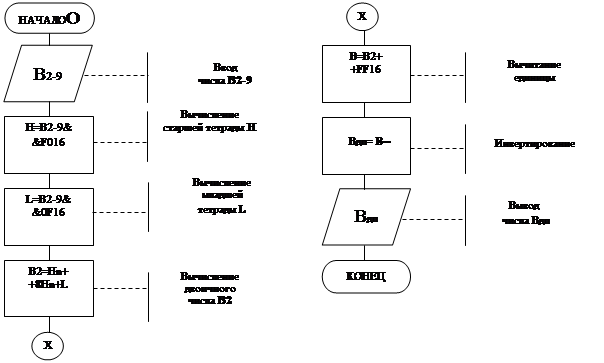Рис.3

Число В поступает кодированное в двоично-девятиричной системе счисления, поэтому старшая тетрада умножается на девять, причём, поступающее число В отрицательно и его прямой код не совпадает с дополнительным. Следовательно, операнд В необходимо перевести в дополнительный код. Это осуществляется путём вычитания единицы с последующим инвертированием. Вычесть единицу можно путем сложения числа с константой вида 1 1 1 1 1 1 1 12 [1].

Всё выше перечисленное показано на рис.3.

2.2.3 Обработка числа С

Для получения числа С необходимо модуль разности чисел А2 и В2 умножить на семь и разделить на четыре. Сумма чисел Адп и Вдп даст результат так же в дополнительном коде. Получить прямой код результата, который будет равен разности чисел А2 и В2, можно при помощи арифметического сложения Сдп с его же знаковыми разрядами:

?????????? ??????? ???? ?? ????????? ???????????? ????? ???????? ?? ?????? ??? ????? ??? ??? ?? ? ??? ????????? ?????????:



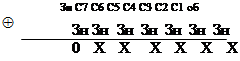Умножение на семь осуществляется следующим способом: 7C= 4C+2C+C. А деление на четыре путём логического умножения на константу 1 1 1 1 1 1 0 02 и задержкой на два такта.

Рисунок 4 представляет схему алгоритма вычисления числа С.