Курсовая работа: Построение траектории Броуновского движения

Рис.5. График гауссовского случайного блуждания

Случайная величина X называется гауссовской, или нормальной с математическим ожиданием µ и дисперсией σ2, если она распределена, но закону:

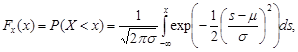
то есть её плотность вероятности f(x) имеет вид:

.

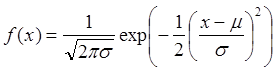График y=f(x) напоминает колокол рис.6. В наших приложениях математическое ожидание обычно равно нулю.

Гауссовское случайное блуждание легко реализуется на компьютере. Единственная сложность― необходим генератор гауссовских случайных чисел. Если имеется генератор, равномерно распределённый на отрезке [0,1] случайных чисел, то вполне приемлемое приближение можно получить, используя формулу:

,

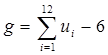Можно использовать и более общую формулу:

,

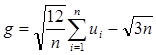0,8
0,6
	0,4
0,2
0
	-0,2
-0,4
	-0,6
-0,8
	-4		-3		-2		-1		0		1		2		3		4

Рис.6. Нормированная гауссовская кривая

3. ОПРЕДЕЛЕНИЕ

Что касается броуновского движения, определенного на конечном интервале, например, на отрезке [а, Ь]. Приведенное ниже определение позволяет сфокусировать внимание на его принципиальных свойствах. Большинство утверждений о броуновском движении относится к одномерному случаю, но имеет соответствующие аналоги для случая двух и большего числа измерений. Прежде всего, нам понадобится определение гауссовского случайного процесса.

Случайный процесс X{t) называется гауссовским, если для каждого конечного набора моментов времени t1, t2, …, tnвектор ( X(t1), X(t2),… , X(tn)) имеет гауссовское распределение. Двумерный гауссовский процесс Х(х; у) определяется аналогично.

Определение: Гауссовский процесс X(t) называется одномерным броуновским движением, или винеровским процессом на интервале [а, Ь], если он обладает следующими свойствами

Х(0) = 0 и функция X(t) почти всегда непрерывна.

Свойство гауссовости приращений: случайная величина

имеет гауссовское распределение с математическим ожиданием и дисперсией где σ — положительная константа, то есть

P(ΔX<x)=

Броуновское движение, как и любой процесс с независимыми приращениями, есть Марковский процесс. Это означает, что условная вероятность события «Х(t2) достигает определённого значения при данном значении Х(t1)», где t1>t2, зависит только от t1 и t2. Эта вероятность не зависит от поведения Х(t), при t<t1, то есть в процессе случайного блуждания каждый шаг делается без какой-либо информации о том, каким образом процесс достиг текущего значения.

Условная вероятность события А при заданном событии В обозначается P(A/B). Формальное определение Марковского процесса:

Где

4. ПРОГРАММИРОВАНИЕ НА DELPH I

Delphi обусловлен как тем, что это наиболее популярная среда программирования, так и объективными несомненными достоинствами.

Среди них:

простой и мощный язык программирования Pascal;

удобная и полная объектная модель;

достаточно удобная среда разработки;