Курсовая работа: Практичне застосування фоторефрактивного ефекту

Рис. 2.4 Схемабезперервноговідновленняголографічноїінтерферограммизусередненнямвчасізвикористаннямзустрічнонаправленогозчитуючогопучка R₂ [13, 14] (а) іголографічнаінтерферограммадифузора, щоколиваєтьсянарізнихчастотах (б, в).

1 — вібруючий об'єкт, 2 — зразок ФРК, 3 — світлодільник, 4 — відікон, 5 — монітор.

У роботі розглянуто два дещо різних варіантів такої схеми: з плоским дзеркалом, що відбиває назад пучок R₁ після проходження ним кристала, і з незалежно формованим зчитуючим пучком R₂ . Перша з них простіша по конструкції і, відповідно, легша в юстируванні, проте накладає жорсткіші вимоги на фазову однорідність кристала і плоскопараллельність його граней. Друга, складніша, допускає отримання оптимального співвідношення між інтенсивністю записуючих і зчитуючих світлових пучків (I_Sl + I_{R 1} ≈ I_{R 2} ), внаслідок чого інтенсивність відновленої інтерферограмми при її використанні виявляється приблизно в 2 рази більшою.

Типовий приклад інтерферограмми вібруючого дифузора, отриманої в, приведений на рис. 2.4, б, в.

3. АДАПТИВНІ ІНТЕРФЕРОМЕТРИ НА ОСНОВІ ФРК

Строго кажучи, термін «адаптивна» в певному значенні може застосовуватися і до звичайної голографічної інтерферометрії, заснованої на використанні стандартних нединамічних фоточутливих середовищ, наприклад звичайних фотоматеріалів. Дійсно, вона дозволяє компенсувати складний рельєф об'єкту, що тестується (тобто адаптуватися до нього) і отримувати інформацію виключно про зміни, що відбулися з ним. У випадку фоторефрактивних кристалів ми матимемо справу з безперервною адаптацією до відносно повільних змін форми хвильового фронту. Як буде показано нижче, це необхідно для оптимальної реєстрації швидких його коливань. Таким чином, очікувані застосування подібної методики лежать в області віброметрії, інтерферометричних .датчиков що швидко змінюються в часі або коливальних процесів і т, д.

Поява цього важливого напряму голографічної інтерферометії практично повністю пов'язана з розробкою і впровадженням високочутливих ФРК.

3.1 Ефект енергообміну фазомодульованих світлових пучків

Нехай зразок ФРК освітлюється інтерференційною картиною двох пересікаючихся плоских когерентних світлових пучків однакової інтенсивності, один з яких промодульований по фазі з деякою частотою Ω (рис. 3.1, а). У випадку, якщо частота коливань значно більша зворотного характерного часу формування голограми у ФРК за даних умов його освітлення (Ω >> τ_sc ^-1 ), голограма не встигає «відстежувати» переміщення інтерференційної картини. Проте вона відображає основний ефект, що полягає в перетворенні початкової фазової модуляції одного із світлових пучків на вході ФРК в амплітудну на його виході.

Очевидно, що в іншому граничному випадку при Ω << τ_sc ^-1 динамічна фазова голограма встигає відстежувати зсуви інтерференційної картини, тобто адаптуватися до неї. Амплітуда голограми і величина фазового зсуву між гратками і картиною виявляються практично не залежними від часу і співпадають зі своїми стаціонарними значеннями. Якщо проводити аналогію з напівпрозорим дзеркалом, використовуваним зазвичай для спостереження биття між двома лазерними пучками, то в даному випадку ми маємо справу з багатошаровим інтерференційним дзеркалом. Останнє, проте, володіє тією важливою властивістю, що положенння і форма його відзеркалювальних поверхонь, відстежуючи зсув смуг інтерференційної картини, тим самим підтримує величину фазового зсуву між пучками S(d) і R(d)), що інтерферують, на виході схеми постійною. Фактично це і приводить до того, що за наявності достатньо повільної фазової модуляції в одному з вхідних пучків світла інтенсивність вихідних пучків підтримується практично на постійному рівні.

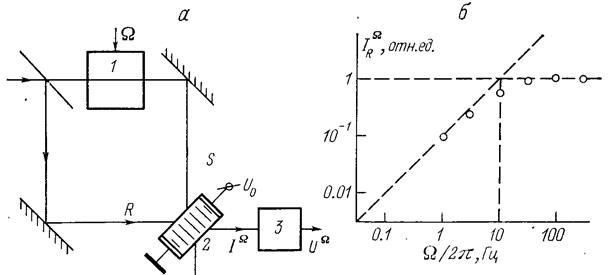
Рис. 3.1 Адаптивний інтерферометр на основі ФРК (a) і його передавальна характеристика (тобто залежність амплітуди вихідного сигналу I_R ^Ω від частоти модуляції F=Ω/2π (б). а: 1 — елемент, в якому здійснюється фазова модуляція снгнального пучка; 2 — зразок ФРК; 3 — фотодетектор, що перетворює модуляцію інтенсивності світлового пучка в електричний сигнал U^Ω .

Докладніший аналіз показує, що за наявності: чисто релаксаційного характеру процесу запису-стирання фазової голограми передавальна характеристика подібного адаптивного перетворювача фаза—амплитуда

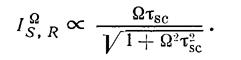(3.1)

Тобто вона співпадає з передавальною характеристикою звичайного радіотехнічногоRС-кола з постійною часу RC, рівною τ_sc .

3.2 Практичні застосування і експериментальні дослідження адаптивних інтерферометрів на основі ФРК

Перш за все слід вказати, що розглянутий ефект «динамічної» самодифракції інтерференційної картини, що коливається, є гарним способом досліджень ФРК [16 -19] і інших динамічних голографічних середовищ. Він вельми простий в юстируванні, не вимагає додаткових зчитуючих пучків і дозволяє визначати як амплітуду гратки і кут фазового розузгодження φ, так і характерний час її запису.

Вперше пропозиція по використанню динамічних голограм у ФРК для цілей адаптивної інтерферометії у волоконно-оптичних датчиках була зроблена в [19]. Автори цієї роботи вказали, що пропонована методика дозволяє використовувати в плечах інтерферометра багатомодові оптичні волокна, значно спростити юстування вихідного вузла інтерферометра, а також забезпечити придушення повільних змін в інтерференційній картині, пов'язаних із зміною зовнішніх умов. Дійсно, у високочутливих волоконно-оптичних датчиках з великою довжиною плечей (10² —10³ м) саме повільний дрейф фазової затримки між плечима інтерферометра через зміну температури або тиску може досягати значної величини (≥10³ рад) [20]. Через істотно нелінійний режим роботи фотоприймача при вказаній величині випадкового фазового зрушення спектр корисного високочастотного сигналу розширюється. Використання динамічної голограми дозволяє компенсувати вказаний повільний дрейф фазової затримки і пропустити практично без ослаблення корисний сигнал в діапазоні -частот Ω≥τ_sc ^-1 .

4. ОБЕРНЕННЯ ХВИЛЬОВОГО ФРОНТУ В НЕЛІНІЙНІЙ ОПТИЦІ

4.1 Поняття про обернену хвилю

Явище інверсії подій в часі має свою аналогію в когерентній оптиці. Нехай лазерний пучок, проходячи через середовище з нерегулярними неоднорідностями показника заломлення, зазнає розсіювання в різних напрямках. Якщо б нам вдалося повернути час назад, то ми побачили б як розбіжний світловий пучок підходить до неоднорідного середовища і, проходячи через нього, “виправляється” до ідеально направленого. В оптиці таку процедуру (інверсія часу) можна здійснити реально.

Існують дві сприятливі обставини реалізації цієї інверсії. По-перше, в лінійній оптиці прозорих середовищ, як геометричній, так і хвильовій, справедливий принцип часової інверсії: рівняння Максвела залишаються інваріантними при заміні знаку часу. Тому для будь-якого розв’язку хвильового рівняння, наприклад для пучка, розсіяного неоднорідним середовищем дійсно існує “обернений” розв’язок того ж рівняння.

По-друге, в оптиці був запропонований і реалізований цілий ряд методів створення оберненої хвилі. В когерентній оптиці дійсно вдається задати такі положення і напрямки, амплітуди і фази елементарних променів, щоб надалі в деталях відтворити поширення оберненої хвилі. Це вдається зробити в тому числі і тому, що когерентний лазерний пучок володіє відносно малим числом ступенів вільності (осциляторів поля), “узагальнені швидкості” яких треба обернути.

Хвильовим фронтом називається гіпотетична поверхня (або сімейство поверхонь), яка визначається умовою постійності фази коливань j(R)=const. Нормалі до цієї поверхні співпадають з променями, які характеризують локальний напрямок хвиль. Пряма і обернена хвилі мають в точності співпадаючі поверхні хвильового фронту, j_об (R)=-const, і поширюються точно назустріч одна одній. У зв’язку з цим операцію отримання оберненої хвилі називають “оберненням хвильового фронту” (ОХФ).

4.2 Практичне використання ОХФ

4.2.1 Двохпровідний підсилювач