Курсовая работа: Применение ЭВМ в технологии лекарственных препаратов

Связь называется ковалентной (гомеополярной), если образующие ее атомы обладают близким сродством к электрону. В этом случае не происходит преимущественной передачи электрона какому-либо атому. Обычно ковалентная связь образуется за счет обобществления электронов, ранее принадлежавших двум отдельным атомам.

Природа ковалентной связи значительно сложнее, чем ионной, и объясняется лишь на основе квантовой механики, причем строго количественное исследование возможно пока что для простейших молекул (Н₂ , Н₂ ⁺ и некоторых других). Для сложных соединений решение уравнения Шредингера производится с помощью приближенных методов, дающих чаще всего только качественные результаты.

К наиболее распространенным методам квантовой химии относятся метод валентных связей (электронных пар) и метод молекулярных орбиталей (МО). Конечная цель обоих методов – нахождение энергии и получение из одноэлектронных атомных волновых функций приближенных волновых функций молекул. Значения Е и ψ должны быть такими, чтобы после подстановки уравнение Шредингера превращалось в тождество. Эти методы в ходе математических расчетов широко отражаются на данные физико-химических исследований свойств молекул.

Метод валентных связей (ВС) разработан Гейтлером и Лондоном (1927) при изучении строения молекулы водорода. Метод основан на предположении, что химическая связь образуется парой электронов в процессе сближения и взаимодействия атомов. Молекулу водорода можно изобразить тремя валентными структурами Н_а – Н_b , Н_а ^- – Н_b ⁺ и Н_а ⁺ – Н_b ^- с различным расположением (смещением) электронной пары. Взаимодействие ядер а и b и электронов 1 и 2 схематически изображено на рис 1. Так как волновая функция ψ зависит от координат двух электронов, то уравнение Шредингера для такой молекулярной системы принимает вид:

, (10)

где и - операторы Лапласа по координатам (χ₁ , y₁ , z₁ ,) первого электрона и координатам (χ₂ , y₂ , z₂ ,) второго электрона.

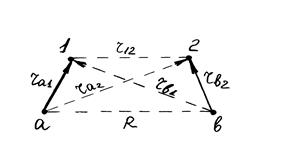
Рис. 1 Схема взаимодействий ядер и электронов в молекуле водорода.

С учетом всевозможных взаимодействий микрочастиц в молекуле Н₂ потенциальная энергия находится из равенства:

, (11)

где первые два члена в скобках выражают соответственно энергии взаимного отталкивания ядер и электронов, остальные – энергии притяжения электронов к ядрам.

Точное нахождение волновой ψ-функции и минимума полной энергии с помощью уравнений (10) и (11) невозможно даже для такой простой двухэлектронной системы, как молекула Н₂ , поэтому используется приближенный метод. Сначала оценивают волновую функцию и энергию изолированных атомов, а далее переходят к системе из связанных атомов.

Обозначим волновые функции двух изолированных атомов φ_а (1) и φ_b (2). Тогда волновая функция ψ_І системы из двух несвязанных атомов выражается произведением ψ_І = φ_а (1) ∙ φ_b (2).

Допустим, что атомы сблизились на расстояние, достаточное для образования химической связи, и что при этом функция ψ_І не изменилась и близка к истинной. Однако в новом состоянии принадлежность каждого электрона к любому из ядер равновероятна, и можно записать, что

ψ_ІІ = φ_а (2) ∙ φ_b (1). Тога ψ_± - функция молекулы Н₂ является линейной комбинацией двух атомных функций:

ψ_± = с₁ ψ_І + с₂ ψ_ІІ , (12)

где с₁ и с₂ – некоторые постоянные.

Уравнение (12) является общим решением уравнения (10). Конкретное его решение состоит в нахождении значений с₁ и с₂ и далее по ψ_± приближенного значения энергии Е_± . Искомую ψ-функцию выбирают с помощью вариационного метода , которые дает

с₁ = ± с₂ и ψ_± = ψ_І + ψ_ІІ .

Функция ψ₊ = φ_а (1)∙φ_b (2) + φ_а (2)∙φ_b (1), не изменяющая знак при перестановке электронов, называется симметричной . Меняющая знак функция ψ_- = φ_а (1)∙φ_b (2) – φ_а (2)∙φ_b (1), называется асимметричной.

Выражение для энергии, которая отвечает функции ψ_± , имеет вид:

, (13)

Уравнение (13) показывает, как должно изменяться значение полной энергии для симметричной и асимметричной функции. Величины J, K и S обозначают три интеграла:

1) кулоновский интеграл J выражает энергию взаимодействия зарядов при отсутствии обмена электронов между ядрами:

,

где можно рассматривать как члены гамильтониана, выражающие взаимодействие между атомами;

2) обменный интеграл К характеризует уменьшение энергии системы, связанное с обменом электронов местами:

;

3) интеграл перекрывания S отвечает перекрыванию волновых функций соединяющихся атомов: