Курсовая работа: Проблематика штучного інтелекту
2.2 Проблема винятків
З успадкуванням пов’язана дуже серйозна проблема – проблема винятків . Вона полягає в тому, що деякі підкласи можуть не успадковувати ті чи інші властивості надкласів. Інакше кажучи, характерні риси класу успадковуються всіма його підкласами, крім деяких .
Нехай відомо, що літають всі птахи, крім пінгвінів (існують деякі інші види птахів, які не літають. Але для наших цілей це не має суттєвого значення). Якби це твердження відразу потрапило до бази знань саме в такому вигляді, особливих проблем не виникало б (хоча і в цьому випадку треба було б передбачити належну обробку винятків).
Але, як було зазначено раніше, експерт не завжди може сформулювати свої знання в явному вигляді. Зокрема, він може не знати або не пам”ятати всіх винятків. Тому він може спочатку включати до бази знань твердження про те, що всі птахи літають, а потім пригадати, що пінгвіни не літають, і додати це до бази знань.
У результаті ми могли б отримати базу знань, подібну до такої:
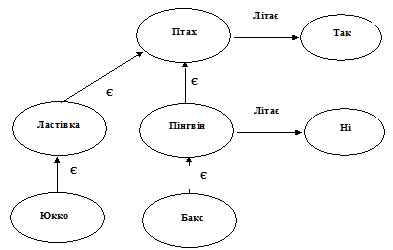
Рис. 1. Ілюстрація наслідування та обробки виключень
Усі птахи літають.
Ластівка є птахом.
Юкко є ластівкою.
Пінгвін є птахом.
Пінгвіни не літають.
Бакс є пінгвіном.
Якби три останні твердження не були включені до бази знань, система просто дійшла б хибного висновку, що Бакс літає. Але включення даних відомостей до бази знань ще більше ускладнює ситуацію. Система знань стає суперечливою: зодного боку, система повинна дійти висновку, що Бакс літає, а з іншого – що Бакс не літає. У даному випадку кажуть про втрату монотонності дедуктивної системи.
Система дедуктивного виведення називається монотонною, якщо виконується така властивість: якщо з набору тверджень (q1,…, qn) випливає твердження v , то v випливає і з набору тверджень (q1,…., qn, r).
Інакше кажучи, в монотонній теорії додавання нових фактів і правил не повинно впливати на істинність висновків, які могли бути отримані без них.
Додавання ж винятків до наявної бази знань може порушити монотонність. Існує багато підходів до вирішення цієї проблеми. Розробляються спеціальні немонотонні логіки : Рейтера, Мак-Дермотта та інші. Проте існують досить прості практичні прийоми. Наприклад, список виключень можна підтримувати явним чином. Інший корисний сформульований прийом : у разі виникнення суперечностей підклас успадковує відповідну властивість лише від найблищого попередника, тобто від класу, найближчого до нього в ієрархії класів.
Далі буде показано, як проблема винятків може вирішуватись в рамках продукційних систем і семантичних мереж.
У семантичних мережах можна також вводити зв’язки, що задають імплікацію, явно.
Слід відмітити, що формалізм семантичних мереж є зручним для задання знань і не дуже зручним для формалізації логічного виведення. Деякі конкретні методи логічного виведення на семантичних мережах описані в [Иск.интел, Вагин, Предст. зн]. Багато з них спираються на механізми дедуктивного виведення, характерні для логічних моделей та продукційних систем (в першу чергу - метод резолюцій). Ряд методик використовує співставлення зі зразком; таке співставлення є більш характерним для фреймових моделей. Але існують і методики, специфічні для семантичних мереж як графових моделей. В основі цих методик лежить інтерпретація логічного виведення та пошуку потрібної інформації в базі знань, яка задана семантичною мережею, як пошуку на графі . Зокрема, в [Предст.зн.] коротко описаний спосіб виведення, який називається перехресним пошуком . Відповідь на запитання формується на основі знаходження та аналізу шляхів між об’єктами, які фігурують у запитанні.
Наприклад, при аналізі мережі, зображеної на рис. 1, на запитання “Що спільного між Баксом та Юкко?” система може відповісти “Обидва вони птахи, але різних видів”.
2.3 Проблема неточних і неповних знань
Раніше ми розглядали проблеми, які необхідно було вирішувати при проектуванні та розробці баз знань. Серед інших проблем можна відмітити такі.Знання можуть бути неповними. Це означає, що для доведення або спростування певного твердження може не вистачати інформації. У багатьох системах логічного виведення прийнято постулат замкненості світу. Це означає, що на запит про істинність деякого твердження система відповідає „так” тоді і тільки тоді, коли його можна довести; якщо ж довести це твердження неможливо, система відповідає „ні”. Водночас „неможливо довести через нестачу інформації” і „доведено, що ні” - це зовсім не одне й те саме. З огляду на це бажано, щоб експертна система запитувала у користувача про факти, яких не вистачає.
Знання можуть бути недостовірними. Наприклад, на результат виконання продукції можуть впливати випадкові чинники (об”єктивна невизначенність) або ж експерт може бути не зовсім впевненим у деякому факті чи правилі виведення (суб”єктивна невизначенність).
Ненадійність знань і недостовірність наявних фактів обов”язково повинні враховуватися в процесі логічних побудов. Звичайно, можна було б просто відкидати факти та првила виведення, які викликають сумнів, але тоді довелося б відмовитися від цінної інформації. Тому необхідно розвивати процедури, які дозволяють здійснювати логічні побудови при недостовірних даних, і використовувати ці процедури в експертних системах. Необхідно враховувати модальність, а саме: необхідність або можливість того чи іншого факту, ставлення суб”єкта до деякого твердження і т.п. Крім того, в таких системах часто доводиться мати справу з неточно визначеними, нечіткими поняттями, такими, як „великий”, „маленький” тощо.
2.4 Деякі проблеми виведення
Нехай ми маємопродукційне правило А=>В (якщо А, то В), при цьому коефіціент упевненості цього правила дорівнює (y ). Зпогляду теорії ймовірностей цей коефіцент упевненості можна проінтерпретувати як Р(В\А) – умовну ймовірність В за умови А.
Нехай коефіціент упевненості твердження А дорівнює (а). Тут ми розглядаємо коефіціенти упевненості окремих тверджень як їх ймовірності.
Чому (в) дорівнює = Р(В) – коефіціент упевненості висновку В? Зразу ж необхідно сказати, що ми не можемо обчислити Р(В) точно – для цього не вистачає інформації. Натомість ми можемо обчислити інтервал, до якого потрапить ця ймовірність.
Очевидно, події А та А складають повну групу подій. Тоді відповідно до формули повної ймовірності маємо: