Курсовая работа: Проект разработки программы-калькулятора CalcKurs на языке программирования Pascal
и делим заданное число на данный множитель, потом ищем следующий простой множитель(если он повторяется, то возводим его в степень), и так до тех пор, пока число не станет равным единице. Записываем все простые множители.
Далее находим все делители числа и составляем из них множество. Вычисляем сумму делителей.
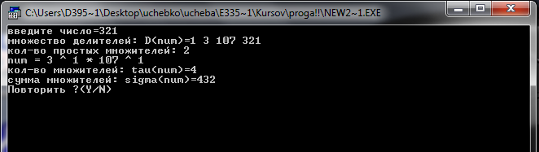
Пример.
Число=21
множество делителей=1 3 7 21
кол-во простых множителей=2
21=3 ^ 1 * 7 ^ 1
кол-во множителей=4
сумма множителей=32
Тесты.
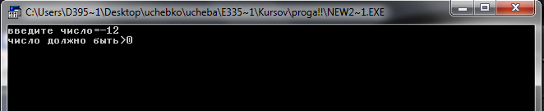
1.Некорректные данные
2.Корректные данные
2.3 NodNok
Назначение.
Данная процедура находит НОД и НОК для заданной совокупности натурального ряда.
Алгоритм.
С помощью алгоритма Евклида (есть числа a,b и последовательность R1>R2>R3>…>RN, где каждое RK - это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело. Тогда НОД(a,b), наибольший общий делитель a и b, равен RN, последнему ненулевому члену этой последовательности) находим НОД[4] для первых двух чисел, «цепляем» следующее число для нахождения следующего НОД, и так до тех пор, пока совокупность чисел не закончится.
Для нахождения НОК первых двух чисел используем следующий алгоритм: разлагаем данные числа на простые множители и к одному из таких разложений приписываем множители недостающие у него против разложений остальных данных чисел[5], и аналогично нахождению НОД «цепляем» следующее число.
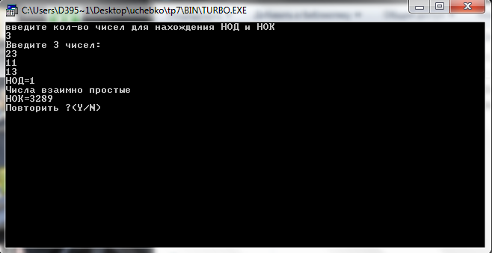
Пример.
Числа: 21 и 12
НОД(12,21)=3
НОК(12,21)=84
Тесты.
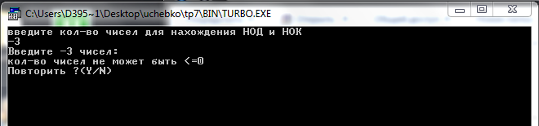
1.Некорректные данные
2.Корректные данные