Курсовая работа: Проектирование аппаратуры передачи данных
Модуляторы, построенные по принципу цифровых, имеют ряд недостатков: сравнительно широкий спектр прямоугольных ЧМ-сигналов, что вынуждает применять сложные ФНЧ высокого порядка; разрыв фазы ЧМ-колебаний, вызываемый изменением информационного сигнала в случайные моменты времени по отношению к окончанию периода колебания на выходе управляемого делителя. Схемы синхронизации являются громоздкими и вызывают дополнительные краевые искажения модулированных сигналов. Более перспективными являются ЧМ-модуляторы со ступенчатой аппроксимацией синусоидального сигнала. В схеме такого модулятора имеется функциональный цифроаналоговый преобразователь (ФЦАП), вход которого соединен с выходом управляемого делителя частоты (УДЧ), а его выход – с ФНЧ. Структурная схема ЧМ-модулятора со ступенчатой аппроксимацией синусоидального сигнала и временные диаграммы его работы представлены на рисунке 3.3.2, а, б. Синусоидальный сигнал формируется kст ступеньками напряжения. Как видно из временной диаграммы, переключение частоты происходит плавно, а краевые искажения сигналов на выходе такого модулятора в kст меньше, чем в модуляторах без ФЦАП. Так как для аппроксимации синусоиды используется четное число ступенек kст , то в спектре такого сигнала будут только нечетные гармоники, ближайшей после первой гармоники будет (kст -1)-я гармоника, следующей – (kст +1)-я и т.д.
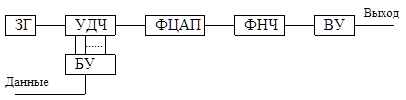
а)
|
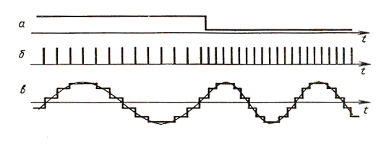
Рисунок 3.3.2 – ЧМ–модулятор со ступенчатой аппроксимацией сигнала: а – структурная схема; б – временные диаграммы
Коэффициент искажения синусоиды за счет аппроксимации Ки определяется на основании спектрального анализа:
Kи = 2π/( kст -![]() ) (3.3.1)
) (3.3.1)
Так как коэффициент искажения синусоидального сигнала должен быть не более 12%, определим необходимое число ступенек аппроксимирующего сигнала
kст ≥ 2π/(Ки ![]() ) = 2π/(0,12
) = 2π/(0,12 ![]() ) = 15,1 (3.3.2)
) = 15,1 (3.3.2)
Округлим kст до ближайшего большего целого четного числа: kст = 16.
Количество ступенек сигнала для прямого и обратного каналов совпадают. Высота i–й ступеньки аппроксимированной синусоиды в относительных единицах определяется по формуле:
Ui = sin [ 360 (i+0,5) / kст ], i = 0,1,2,…, ( kст - 1 ) (3.3.3)
Рассчитав данные значения, построим ступенчатую аппроксимацию синусоидального сигнала, изображенную на рисунке 3.3.3.
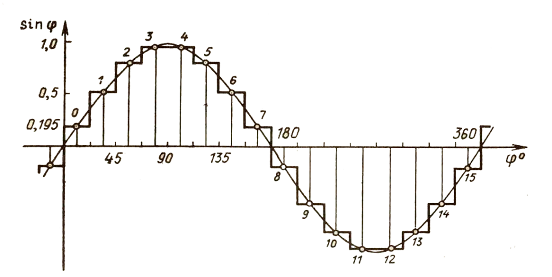
Рисунок 3.3.3 – Ступенчатая аппроксимация синусоидального сигнала
При использовании ИМС более высокой степени интеграции, а также в микропроцессорных УПС для формирования синусоидальных сигналов целесообразно использовать построенное запоминающее устройство (ПЗУ) и цифроаналоговый преобразователь (ЦАП). Обычно каждый из этих функциональных узлов выполняется в виде отдельной ИМС. Схема преобразования цифровой последовательности в синусоидальный сигнал приведена на рис 3.3.4. Адресная шина ПЗУ подключается к выходам двоичного счетчика СТ2, вход которого соединен с выходом УДЧ модулятора, либо к адресной шине микропроцессора УПС. В ячейки ПЗУ в цифровом виде заносятся значения напряжений синусоиды, соответствующие своим фазовым углам ∆φ (см. рис. 3.3.3) Количество слов, хранимых в ПЗУ, равно kст . Емкость ПЗУ можно уменьшить до kст/4, при этом существенно усложнится схема формирования адресов. Разрядность слова ПЗУ np зависит от точности воспроизведения ступенчатого напряжения. На практике достаточно принять np=8 с учетом знакового разряда, что обеспечивает погрешность формирования напряжения менее 1%.
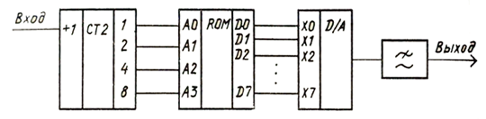
Рисунок 3.3.4 – Цифровой формирователь синусоидальных сигналов на основе ПЗУ
В микропроцессорных УПС адресации ПЗУ осуществляется программным способом. Время нахождения адреса ta на соответствующей шине микропроцессора определяется программой и зависит от частоты формируемой синусоиды fi вых выходного сигнала
ta = 1/( fi вых kст) (3.3.4)
3.4 Разработка приемной части УПС
Структурная схема приемной части УПС изображена на рисунке 3.4.1
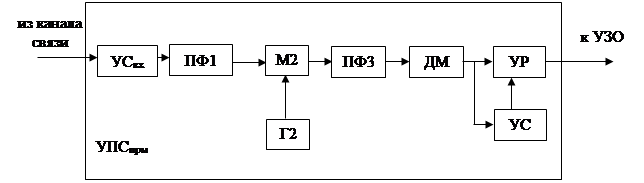
Рисунок 3.4.1 – Структурная схема приемной части УПС
Демодуляторы ЧМ-сигналов современных систем передачи данных строятся преимущественно на цифровых элементах. Входной сигнал в схеме демодулятора преобразуется в прямоугольную последовательность импульсов, постоянная составляющая которой зависит от частоты демодулируемого колебания. Помехоустойчивость таких демодуляторов несколько ниже, чем у частотных дискриминаторов с колебательными контурами. Высокая стабильность параметров схемы, отсутствие необходимости регулировок в процессе эксплуатации обусловили широкое применение их на практике.
Функциональная схема одного из вариантов ЧМ – демодулятора приведена на рисунке 3.4.2. В её состав входит усилитель-ограничитель (УО) с нулевым порогом ограничения, формирователь коротких импульсов в моменты переходов входного сигнала через нуль (ФКИ), одновибратор (ОВ), фильтр низких частот (ФНЧ) и пороговое устройство (ПУ). Временная диаграмма, иллюстрирующая работу ЧМ- демодулятора, показана на рис. 3.4.3. Импульс фиксированной длительности формируется ОВ в момент пресечения входным сигналом нулевого уровня. Длительность импульса должна быть меньше длительности периода верхней частоты демодулируемого сигнала. Из прямоугольной последовательности импульсов ОВ ФНЧ выделяет постоянную составляющую, которая преобразуется ПУ в посылки постоянного тока.

|
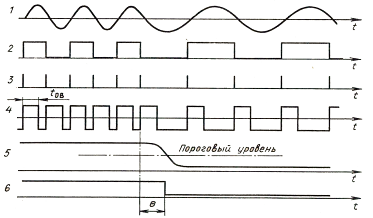
Рисунок 3.4.3 – Временные диаграммы ЧМ–демодулятора
Для формирования коротких импульсов целесообразно использовать схему цифрового дифференциального выпрямителя (см. рис 3.4.4). В качестве ОВ можно применить схему ждущего мультивибратора, выполненного на логических элементах или на основе счетчика импульсов с предварительной установкой. Принцип действия ОВ на основе счетчика заключается в том, что импульсом нулевого пересечения в счетчик заносится число, в результате чего на его выходе появится положительный потенциал, длительность которого определяется выбором заносимого в счетчик числа, емкостью счетчика и частотой следования тактовых импульсов. Схема ОВ на основе счетчика будет более громоздкой, но стабильность параметров импульса значительно выше.