Курсовая работа: Проектування блоку обробки сигналів

Рис. 2.2.23. Сигнал після та до фільтрації

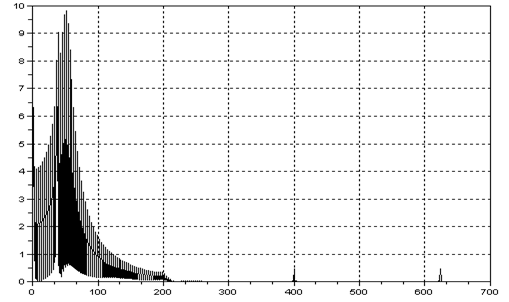
Рис. 2.2.24.АЧХ сигналу після фільтрації

Середньоквадратичне значення похибки між ідеальним та відфільтрованими сигналами дорівнює 0.0681289.

Отже, найменшу похибку між ідеальним та відфільтрованим сигналами дає обернений фільтр Чебишева, також він забезпечує найкращу форму сигналу, найближчу до ідеального, тому цей фільтр використаємо для фільтрації сигналу.

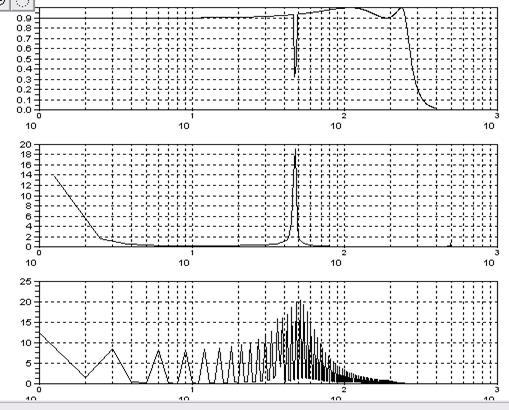
Рис. 2.2.25. АЧХ фільтра, завади та корисного сигналу.

Висновки

В результаті виконання курсового проекту був спроектований цифровий фільтр для очистки сигналу від завади. Було знайдено найбільш оптимальне рішення цієї задачі при послідовному з’єднанні фільтрів. Найменша середньоквадратична похибка дорівнювала 0.0662035. Отримані фільтри можна використовувати, написавши відповідну програму.

Список викорикористаної літератури

1. В. Дьяконов MatLab. Обработка сигналов и изображений. Специальный справочник. – СПб.:Питер, 2002.

2. Л. М. Гольденберг, Б.Д.Матюшкин, М.Н.Поляк. Цифровая обработка сигналов:Справочник . М.:Радио и связь, 1985.

3. http://matlab.exponenta.ru/default.php

4. Internet

Додаток

Лістінг програми при послідовному ввімкненні фільтрів:

clear all

clc

loadmatfile('kasE.mat')

//scf(1)

//plot(ys)

//xgrid()

//

scf(2)

plot(f(1:n2),amp(1:n2))

xgrid()

//

//scf(3)

//subplot(211), plot(ys), xgrid()