Курсовая работа: Проектування керуючих автоматів Мура та Мілі за заданою граф-схемою алгоритму
Одержуємо мінімальну диз’юнктивну нормальну форму (МДНФ):
у = ![]()
Для знайденої форми обчислимо ціну за Квайном, яка дорівнює додатку кількості слагаємих, кількості елементів та кількості заперечень.
Цкв. = 25
МКНФ:
|
х1 х2 х3 х4 х5 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
 00 00 | Х | 1 | 0 | 0 | Х | 1 | 1 | |
  01 01 | 1 | 1 | 0 | 0 | 1 | Х | Х | 1 |
 11 11 | 0 | 1 | 1 | 0 | 1 | Х | 0 | 0 |
| 10 | 0 | Х | 1 | 1 | Х | 1 | 0 |
Одержуємо мінімальну кон’юктивну нормальну форму (МКНФ):
у = 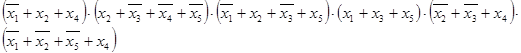
Для знайденої форми обчислимо ціну за Квайном, яка дорівнює додатку кількості помножень плюс один, кількості елементів та кількості заперечень.
Цкв. = 39
Виходячи з того, що ціна по Квайну МДНФ функції менше, ніж МКНФ, обираємо для реалізації МДНФ функції. Реалізацію будемо проводити згідно з заданим базисом 2ЧИ-НІ. Застосуємо до обраної форми факторний алгоритм та одержимо скобкову форму для заданої функції:
у = ![]()
у = ![]()
у = ![]()
2. Вибір блоків та структури ГСА
Граф-схеми алгоритмів обираються кожним студентом індивідуально. Граф-схема складається з трьох блоків E, F, G і вершин «BEGIN» і «END». Кожен блок має два входи (A, B) і два виходи (C, D). Студенти вибирають блоки E, F, G з п'яти блоків з номерами 0, 1, 2, 3, 4 на підставі чисел А, В, С за такими правилами:
– блок Е має схему блока під номером (А) mod5;
– блок F має схему блока під номером (В) mod 5;
– блок G має схему блока під номером (С) mod 5.
Блоки E, F, G з'єднуються між собою відповідно до структурної схеми графа, що має вид
– для групи АН-042;
 |