Курсовая работа: Проектування комбінаційних схем на мікросхемах різного ступеню інтеграції
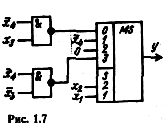
рис. 1.7
Визначення варіанту завдання
Синтез комбінаційної схеми на логічних елементах можна умовно розбити на три етапи.
Визначаємо варіант перемикальної (больової) функції. Для цього номер варіанту переводимо у двійкову систему числення і записуємо шість його молодших розрядів у вигляді: a6 a5 a4 a3 a2 a1 .
54 (110110): a6 =1, a5 =1, a4 =0, a3 =1, a2 =1, a1 =0.
Визначивши значення ai , підставляємо їх у таблицю 1.1.
Таблиця 1.1
 |  |  |  |  |  |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
.
.
На першому етапі, виходячи з таблиці істинності перемикальної функції, що описує роботу синтезованої комбінаційної схеми, знаходять мінімальну диз'юнктивну нормальну форму (МДНФ) функції (чи її заперечення).
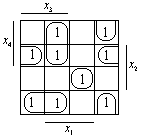
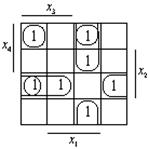
Для заданої функції і для її заперечення знаходимо МДНФ за допомогою діаграми Кароно–Вейча.
.
МДНФ: 
.
.
МДНФ:
.
Якщо функція, що описує роботу синтезованої схеми, є частково визначеною (заданою не на всіх 2n наборах), то попередньо роблять оптимальне її до визначення (таке, при якому функція буде мати більш просту МДНФ). На цьому перший етап закінчується.
На другому етапі функцію записують у так називаної операторній формі, тобто у вигляді суперпозиції операторів логічних елементів. Оператором логічного елемента називають функцію, що реалізується цим елементом. Якщо число входів в операторах досить велике, то одержання операторного запису функції зводиться до її представлення в одній зі стандартних канонічних нормальних форм. Таких форм вісім.
Узявши подвійне заперечення МДНФ функції і затосувавши кілька разів правило ДеМоргана, одержуємо нормальні форми:
і/ні
і-ні/і-ні
або/і-ні
або-ні/або
і/або-ні
і-ні/і
або/і
