Курсовая работа: Проектування нової конструкції шнекової фрези

1. Первинна похибка через проходження між справжнім значенням фізичної величини і її розрахунковим значенням, прийнятим для здійснення на моделі;

2. Друга похибка - через неточність відтворення на моделі модельованих величин (розрахункових значень) і похибок, зв’язаних з розмірами;

3. Принципова похибка – через неповного врахування в моделі факторів які заздалегідь впливають на вивчаючі процеси (наприклад, обумовленим моделюванням замість точного).

В інструментальному виробництві фізичне і математичне моделювання використовується для того,щоб наперед оцінити ефективність нових конструкцій ріжучого інструменту і визначити оптимальні параметри,які забезпечать максимальну стійкість.

Різальні властивості любого інструменту визначаються в процесі різання на основі порівняння результатів цього процесу з якими-небудь іншими показниками. Фізичне моделювання дає можливість замінити складний різальний інструмент більш простим і розглядати замість реального процесу роботи складного інструмента на більш простий. Можливі і інші способи фізичного моделювання процесу.

Математичним моделюванням можна визначити ефективність нової конструкції інструмента до його виготовлення. Крім цього кореляційне рівняння залежності стійкості від деяких параметрів інструмента і умов різання також можна використати як математичні моделі роботи різальних інструментів. Ці рівняння прораховують на ЄВМ і визначають оптимальну комбінацію параметрів які забезпечують необхідну стійкість інструменту.

Любу модель можна оцінити тільки на основі встановлення тісного кореляційного зв’язку між результатами роботи реального інструменту в звичайних виробничих умовах і результатами ,які отримані при моделюванні.

Для оцінки моделі можна використовувати коефіцієнт кореляції. Якщо X1 iX2 випадкові величини,взяті фіксовані моменти часу t1 it2 то коефіцієнт кореляції.

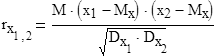
Де М – символ математичного очікування;

D – символ дисперсії;

Коефіцієнт кореляції є мірою залежності випадкових величин X1 iX2.В випадку незалежності цих величин r = 0.Якщо X1 iX2 зв’язані точною лінійною залежністю, то r=±1. Відповідно,величини X1 iX2 будуть некорильовані, якщо r = 0,и корельовані, якщо .

3. Проектування нової конструкції зуборізної шнекової фрези

3.1 Аналіз завантаження зуборізної фрези

Роботоздатність різального інструменту можна підвищити, поліпшивши розподілення навантаження на різальні леза і оптимізувавши геометричні параметри і умови різання.

При проектуванні нових конструкцій металорізальних інструментів необхідно визначити можливий ефект від їх введення. Таку оцінку нової конструкції бажано зробити перед (розрахунковим шляхом) виготовленням самого інструменту. Розглянемо на прикладі оцінки нової конструкції зуборізної черв’ячної фрези.

Дослідження і аналіз роботи стандартних циліндричних черв’ячних фрез показує, що загрузка на зуби роз приділяється нерівномірно .Це призводить до того,що до повного зносу доводиться тільки невелика частина загального периметра різальних зубців. При фрезеруванні основний об’єм металу зрізується вершинами зубців, тому проблема покращення загрузки зуборізних фрез повинна вирішуватись в першу чергу за рахунок перерозподілення загрузки вдовж вершинних ріжучих кроком.

Одним з можливих шляхів вирішення цієї задачі є застосування конічних черв’ячних фрез, призначених для обробки циліндричних зубчастих коліс.

3 .2 Створення математичної моделі для дослідження завантаження

зуборізної шнекової фрези

Попередню оцінку загрузки фрез проведемо методом математичного моделювання. В якості моделей приймемо поверхні обертання верхніх різальних кромок, які відповідають вершинам зубців,навкруг осі фрези, тобто модель стандартної черв’ячної фрези буде циліндрична фреза,а моделлю конічна кутова фреза.

Інтенсивність завантаження,і відповідно зносу визначається товщиною зрізу,швидкістю різання,часу контакту з заготовкою і «відпочинку» досліджуваної точки різальної кромки. Знаючи вказані параметри, можна зробити висновок про ступінь нерівномірності завантаження різальної кромки.

Товщина шару, який зрізується при зубофрезеруванні, визначається як переміщення різальної кромки в тіло заготовки по нормалі до поверхонь різання за час між двома зрізами. Вказаний час приблизно дорівнює часу повороту фрези навкруг своєї осі на один зуб.

Вектор відносної швидкості руху випадкової точки вершинної різальної кромки конічної фрези позначається ,а одиничний вектор нормалі до поверхні різання .

Тоді проекція вектора відносної швидкості на нормаль до поверхні різання буде скалярне відображення названих векторів:

[1]

Визначимо координати закінчення вектора відносно швидкості для випадкової точки М,розташованій в січенні ri на відстані с від середнього діаметра конічної фрези (рис.4. 1 ).

Вісь інструменту позначимо Ои, вісь заготовки – Оз, кут встановлення фрези - ψ, кут нахилу початкового конусу – β. Положення точки М відносно горизонтальної площини, яка проходить через вісь інструменту, характеризується кутом повороту θ. Виберемо систему координат xyz.

Початок координат розташуємо в точці М. Вісь х направимо паралельно осі інструменту Ои, вісь у – по дотичній до січення в точці М.