Курсовая работа: Программа "Крестики-нолики 5 в ряд на неограниченном игровом поле"

Возвращаемое значение:

Нет.

Алгоритм работы:

Изменяется значение переменной comp_level. Значение коэффициента агрессивности игры компьютера attack_factor устанавливается в 1. Вызывается функция new_game для начала новой игры. Выполняется перерисовка окна.

5. Алгоритм работы программы

Алгоритм выполнения очередного хода:

Игрок выполняет очередной ход при нажатии левой кнопки мыши на игровом поле. При этом вызывается функция обработчика OnLButtonDown, которая содержит основной алгоритм выполнения очередного хода игроком и компьютером. Алгоритм работы функции приведен на рисунке 1.

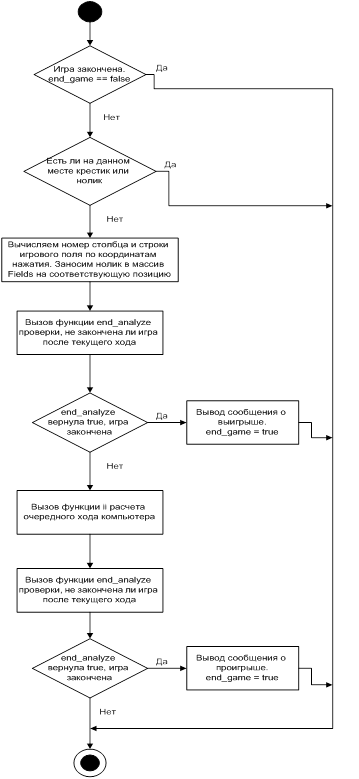
Рисунок 1 – Блок-схема работы функции OnLButtonDown.

Алгоритм расчета очередного хода компьютерного соперника:

Расчет очередного хода компьютерного соперника выполняется при помощи вызова функции ii. Расчет производится при старте игры, если приоритет хода принадлежит компьютеру или после хода игрока вызовом из функции OnLButtonDown.

Расчет производится по следующему алгоритму:

1) Рассчитывается суммарная оценочная функция для всех непустых клеток игрового поля. Под оценочной функцией понимается некое значение, присваиваемое клетке и обозначающее выгодность хода в данную клетку.

Расчет производится при помощи функции calculate, которая позволяет рассчитать оценочную функцию для отдельной клетки в случае хода в эту клетку игроком или компьютером.

Суммарная оценочная функция вычисляется по формуле:

, где

– значение суммарной оценочной функции;

– значение оценочной функции при постановке в клетку крестика, рассчитанное с помощью вызова функции calculate;

– значение оценочной функции при постановке в клетку нолика, рассчитанное с помощью вызова функции calculate;

– коэффициент агрессивности ИИ, задается переменной attack_factor.

Как видно из формулы, значение суммарной оценочной функции учитывает выгоду как своего хода в данную клетку, так и выгоду, которую получил бы соперник от хода в данную клетку. Причем чем больше коэффициент агрессивности, тем больше учитывается выгода соперника и соответственно компьютерный игрок следует защитной стратегии.

Значение коэффициента агрессивности на уровнях новичок и профессионал равно 1, компьютер ведет себя агрессивно. На уровне любитель значение равно 10, алгоритм находится в глубокой обороне.

Для уровней новичок и любитель также дополнительно вносится случайность значения суммарной оценочной функции: на уровне новичок значение суммарной оценочной функции умножается на случайное число, принимающее значение [0,1], на уровне любитель умножается на случайное число, принимающее значение [0.5,1].

2) Находится клетка с максимальным значением суммарной оценочной функции. Если таких клеток несколько, то из них выбирается случайная. Ход делается в найденную клетку, массив fields обновляется путем установки соответствующего элемента в значение 2.

Алгоритм расчета оценочной функции:

Расчет оценочной функции для клетки игрвого поля производится вызовом функции calculate. Входными параметрами являются индексы поля в массиве fields (текущая клетка) и идентификатор, какой символ(крестик или нолик) будет поставлен в текущую клетку. Этот символ временно ставится в массив fields до окончания работы функции.

Расчет производится по следующей схеме. Просматриваются все ряды, продолжением которых может являться текущая клетка. Под рядом подразумевается последовательность из 5 клеток, каждая из которых может быть пустой или содержащей такой же символ, как и в текущей. Для этого проходятся все клетки на расстоянии не более 4 от данной, сначала по вертикали, затем по горизонтали, затем по 2 диагоналям. Для каждой проходимой клетки рассчитывается длина ряда, в которую она входит вместе с текущей. Под длиной ряда понимается количество одинаковых символов(крестиков или ноликов) в последовательности из 5 клеток. Если ряд прерывается противоположным символом, то длина ряда принимается равной нулю.

Значение оценочной функции рассчитывается по формуле:

, где – общее количество ненулевых длин рядов;