Курсовая работа: Программирование на сетях

где j – конечные вершины ребер, исходящих из I;

i – начальные вершины ребер, входящих в S.

Линейную функцию f называют мощностью потока на сети. Сформулируем задачу о максимальном потоке: найти множество XP^{* P} = {xB_ijPB ^*P } потоков xB_ijPB ^*P по всем ребрам (i,j) сети, которое удовлетворяет условиям (1.1) - (1.3) и доставляет линейной функции (1.4) максимальное значение.

Как видно из формулировки, это типичная задача линейного программирования.

Обратимся к рис. 1.8, где изображена сеть. Для этой сети пропускную способность представим в виде матрицы, используя цифры в скобках. Здесь n = 6 и числа образуют квадратную матрицу шестого порядка (табл. 1.1). Если вершины k и l не соединены, то rB_{kl B} = rB_lkB = 0. Сформировать матрицу чисел xB_ijB – это значит задать поток на сети, т.е. найти nP^{2 P} чисел, удовлетворяющих условиям (1.1) – (1.3). Рассмотрим полный путь 1 – 2 – 5 – 6.

Пропускная способность этого пути не больше 1 ед. и ограничивается ребром (2, 5), которое лежит на этом пути. Поток по этому пути мощностью в 1 ед. будет допустимым, и условии (1.1) – (1.3) должны выполняться для всех вершин и ребер этого пути.

Таблица 1.1

i/j	1	2	3	4	5	6
1	0	3	6	2	0	0
2	5	0	0	0	1	0
3	6	0	0	3	0	4
4	7	0	9	0	4	0
5	0	1	0	2	0	5
6	0	0	1	0	8	0

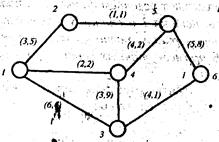
Рис. 1.8

Например, возьмем вершину 2 и проверим условие (1.3):

xB_21B + xB_25B = (-xB_21B ) + xB_25B = (-1) + 1 = 0.

5. Разрез на сети

Представим некоторую сеть. Разобьем множество вершин сети на два непересекающихся подмножества A и B так, чтобы исток I попал в подмножество A, а сток S попал в подмножество B. В результате такого разбиения появляются ребра (i, j), конечные точки которых оказываются в разных подмножествах.

Совокупность ребер (i, j), начальные точки которых принадлежат подмножеству A, а конечные точки – подмножеству B, называют разрезом сети и обозначают A/B.

На рис. 1.9 изображена некоторая сеть. Стрелки указывают положительное направление потока. На сети произведено два разреза: I и II. При разрезе I образовалось два подмножества вершин сети: подмножество A = {1, 2} и B = {3, 4, 5}, а ребрами, образующим разрез, стали (1, 3), (1, 4), (2, 4). При разрезе II образовались подмножества A = {1, 2, 3, 4} и B = {5} с образующими разрез ребрами (3, 5) и (4, 5).

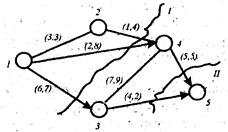
Рис. 1.9

Величина , представляющая сумму пропускных способностей всех ребер разреза, называется пропускной способностью разреза.

Если на сети задан поток X = {xB_ijB } и разрез (A/B), то величина , представляющая сумму потоков по всем ребрам разреза, называется потоком через разрез.

Дляразреза I R(I) = rB_13B + rB_{14 B} + rB_24B = 6 + 2 + 1 = 9. X(I) = xB_13B + xB_14B + xB_24B = 4 + 2 + 0 = 6. Для разреза II – R(II) = 9, X(II) = 6.

В общем случае, если на сети задан поток X = {xij} и произведен разрез (A/B), то хотя бы одно ребро любого полного пути, идущего из истока в сток, будет обязательно принадлежать разрезу (A/B). Напомним, что величина потока по любому полному пути не превышает пропускную способность каждого его ребра, а потому величина X суммарного потока, стремящегося из истока в сток, не может повысить пропускную способность любого разреза сети, т.е.

(1.5)

В теории потоков утверждается, что если удастся построить на сети поток XP^{* P} = {xB_ijPB ^*P }, величина которого равна пропускной способности некоторого разреза (A/B), то этот поток будет максимальным, а разрез обладать минимальной пропускной способностью. Ниже приводится теорема о максимальном потоке, имеющая большое прикладное значение.

Теорема Форда - Фалкерсона. На любой сети сети максимльная величина потока из истока I в исток S равна максимальной пропускной способности разреза, отделяющего I от S.

6. Алгоритм решения задачи о максимальном потоке

В разделе 4 был проведен расчет мощности потока, но ничего не было сказано о том, будет ли этот поток максимальным. Чтобы ответить на этот вопрос, необходимо исследовать этот поток.

Пусть задан некоторый поток X = {xij}. Разобьем сеть таким образом, чтобы к подмножеству A отошли исток I и все те вершины i, которые достигаются из истока I хотя бы по одному пути, состоящему из ненасыщенных ребер; к подмножеству B отнесем вершины, которые нельзя достичь из истока по ненасыщенным ребрам. При таком разбиении возникают две ситуации:

1) сток ;

2) сток .