Курсовая работа: Расчет фильтра нижних частот
 ,
,  и т.д.
и т.д.
где 
т.е. в рассматриваемом примере  и т.д.
и т.д.
Далее для каждого звена определяем параметр ![]() и частоту минимального затухания:
и частоту минимального затухания:
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Частота последнего минимума затухания должна совпадать с верхней граничной частотой полосы задерживания. Кроме того должно соблюдаться строгое чередование частот бесконечного и минимального затухания. Правильность расчета подтверждается в рассматриваемом примере равенством и таблицей 1.
![]()
Таблица 1
| Частота, кгц | 1 звено | 2 звено | 3 звено | 4 звено |
| 310,442 | 139,356 | 119,137 | 115,313 | |
| 176,369 | 125,179 | 116,4189 | 115 |
Заметим, что наибольшему значению m соответствует наиболее удаленная от полосы пропускания частота бесконечного затухания, а наименьшему значению m соответствует ближайшая к переходной области частота бесконечного затухания. Все частоты ![]() и
и ![]() находятся в полосе задерживания. Не допускается расположение частот
находятся в полосе задерживания. Не допускается расположение частот ![]() и
и ![]() в полосе пропускания.
в полосе пропускания.
Определив частоты бесконечного и минимального затухания, а так же значения коэффициентов ![]() для всех звеньев и составив полную принципиальную схему фильтра нижних частот (ФНЧ состоит из трех звеньев типа 1В1н и двух полузвеньев типа 2А1н), приступаем к расчету номинальных значений элементы схемы ФНЧ. Начинаем с определения величины расчетного сопротивления
для всех звеньев и составив полную принципиальную схему фильтра нижних частот (ФНЧ состоит из трех звеньев типа 1В1н и двух полузвеньев типа 2А1н), приступаем к расчету номинальных значений элементы схемы ФНЧ. Начинаем с определения величины расчетного сопротивления 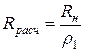 , а затем единичной индуктивности
, а затем единичной индуктивности ![]() и единичной емкости
и единичной емкости ![]() .
.
Коэффициент нагрузки ![]() рассчитывается графоаналитическим способом. Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).
рассчитывается графоаналитическим способом. Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).
Таблица 2
| Оконечное полузвено | ||||||
| f, кгц | 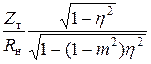 | 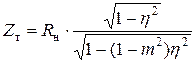 | 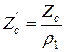 | |||
| 50 | 0,4424 | 0,8968 | 0,87128 | 1,02929 | 1029,29 | 1,03592 |
| 55 | 0,4867 | 0,8736 | 0,84421 | 1,0348 | 1034,8 | 1,0415 |
| 60 | 0,5309 | 0,8474 | 0,8146 | 1,04027 | 1040,27 | 1,04697 |
| 65 | 0,5751 | 0,81805 | 0,7825 | 1,0454 | 1045,4 | 1,0521 |
| 70 | 0,6194 | 0,7851 | 0,7477 | 1,0500 | 1050,0 | 1,0568 |
| 75 | 0,6636 | 0,7481 | 0,71037 | 1,05311 | 1053,11 | 1,053865 |
| 80 | 0,7079 | 0,7064 | 0,6704 | 1,05369 | 1053,69 | 1,0605 |
| 85 | 0,7521 | 0,6590 | 0,62797 | 1,0494 | 1049,4 | 1,0562 |
| 90 | 0,7964 | 0,6048 | 0,58285 | 1,03766 | 1037,66 | 1,0443 |
| 95 | 0,8406 | 0,5417 | 0,53526 | 1,01203 | 1012,03 | 1,01855 |
| 100 | 0,8848 | 0,4659 | 0,48511 | 0,9604 | 960,4 | 0,9666 |
Коэффициент согласования ![]() – это отношение характеристического сопротивления к сопротивлению нагрузки, т.е.
– это отношение характеристического сопротивления к сопротивлению нагрузки, т.е. ![]() . Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой
. Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой ![]() относительно значения
относительно значения ![]() (т.е. уравнивания наибольшего и наименьшего значений
(т.е. уравнивания наибольшего и наименьшего значений ![]() в полосе пропускания).
в полосе пропускания).
Исходя из этого, определяется коэффициент нагрузки ![]() , позволяющий затем вычислить
, позволяющий затем вычислить ![]() как оптимальное номинальное характеристическое сопротивление. Проводя симметрирование, перемещаем кривую
как оптимальное номинальное характеристическое сопротивление. Проводя симметрирование, перемещаем кривую 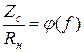 вдоль оси ординат относительно значения
вдоль оси ординат относительно значения ![]() (в рассматриваемом примере вниз) так, чтобы максимальное положительное и максимальное отрицательное отклонения функции
(в рассматриваемом примере вниз) так, чтобы максимальное положительное и максимальное отрицательное отклонения функции ![]() от значения
от значения ![]() были приблизительно равны.
были приблизительно равны.
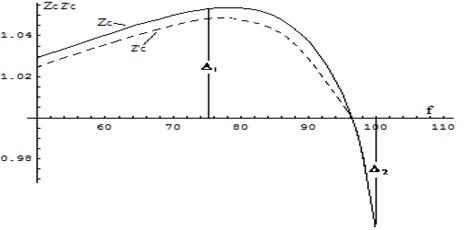
Рисунок 9 – График симметрирования характеристического сопротивления ФНЧ
В рассматриваемом примере экспериментальное значение функции ![]() соответствует значениям
соответствует значениям ![]() и
и ![]() . На частоте
. На частоте ![]() коэффициент согласования
коэффициент согласования ![]() . На частоте
. На частоте ![]() коэффициент согласования
коэффициент согласования ![]() .
.
Из этого обобщенного графика можно сделать заключение о форме характеристики затухания фильтра нижних частот. Положительное отклонение 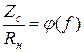 от значения
от значения 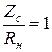 свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот
свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот ![]() и
и ![]() ; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).
; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).
Максимально положительное и максимально отрицательное отклонение на этих частотах составляют соответственно (![]() )
)
![]()
![]()
Разность отклонений
![]()
Среднее отклонение
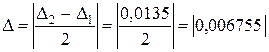
Новое значение коэффициента согласования на частоте ![]() с учетом среднего отклонения
с учетом среднего отклонения
![]()
Коэффициент несогласованности ![]() и коэффициент нагрузки
и коэффициент нагрузки ![]() на частоте
на частоте ![]() соответственно равны
соответственно равны