Курсовая работа: Расчет и моделирование цифрового фильтра

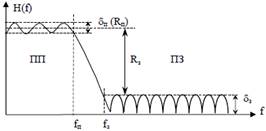
Рис. 3 Реальная АЧХ цифрового фильтра (на примере ФНЧ).

Математически работа цифрового фильтра во временной области описывается разностным уравнением:

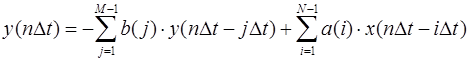, (1)

где и - - тые отсчеты входного и выходного сигналов фильтра, взятые через интервал ; и – постоянные коэффициенты цифрового фильтра.

Цифровые фильтры принято делить на два класса:

− нерекурсивные фильтры;

− рекурсивные фильтры.

Нерекурсивные фильтры называют еще фильтрами с конечной импульсной характеристикой (КИХ-фильтры), а рекурсивные фильтры - фильтрами с бесконечной импульсной характеристикой (БИХ-фильтры). В иностранной литературе их называют:

− FIR (Finite Impulse Response) – фильтр с конечной импульсной характеристикой;

− IIR (Infinite Impulse Response) – фильтр с бесконечной импульсной характеристикой.

Если в выражении (1) положить коэффициенты , то фильтр, реализующий этот алгоритм, называется нерекурсивным. Его работа описывается уравнением:

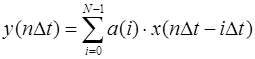, (2)

вычисляющим свертку двух последовательностей: коэффициентов и дискретных отсчетов входного сигнала .

Если хотя бы один коэффициент , то фильтр, реализованный согласно выражения (1), называется рекурсивным. Очевидно, что БИХ-фильтр представляет собой устройство с обратной связью, а КИХ-фильтр - без обратной связи.

Общие сведения по КИХ-фильтрам

Нерекурсивные фильтры работают в соответствии с выражением (2). Раскроем сумму:

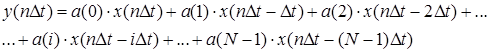(3)

КИХ-фильтр производит взвешенное суммирование (с коэффициентами ) предшествующих отсчетов входного сигнала. Величину называют порядком фильтра, – шаг дискретизации. Структурная схема КИХ-фильтра представлена на рис. 4.

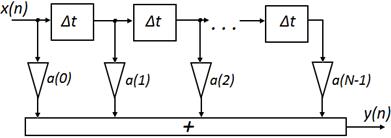
Рис. 4 Структурная схема КИХ-фильтра.

В этом фильтре дискретные выборки из сигнала , задержанные на интервалы , взвешиваются с коэффициентами и суммируются с образованием отклика . Фильтр, представленный на рис. 4 называют еще трансверсальным фильтром. Основными элементами фильтра являются:

− линия задержки с отводами;

− умножителей;

− многовходовый параллельный сумматор.

КИХ-фильтры всегда устойчивы. Форма частотной характеристики КИХ-фильтров слабо чувствительна к точности коэффициентов. Главным преимуществом КИХ-фильтра является линейность его ФЧХ.

Z - преобразование (3):

. (4)

Тогда передаточная характеристика КИХ-фильтра:

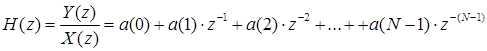. (5)