Курсовая работа: Расчет кривошипного механизма

Fn30= F30=4400(H); Fn21=F21=3200(Н).

2.4 Определение уравновешивающей силы

Определение уравновешивающей силы проводится двумя методами:

Нахождение уравновешивающего момента непосредственно из уравнений равновесия ведущего звена.

Определение уравновешивающей силы и момента с помощью “рычага” Жуковского.

Определим уравновешивающую силу и её момент по первому методу.

Прикладываем к точке А силу F12 равную по модулю ранее найденной силе F21 но противоположную ей по направлению.

Составим уравнение моментов относительно точки О1.

Мур=F12×hF12×ml (2.24)

Мур=3200×85×0,003=816(Нм)

Определим уравновешивающую силу и её момент с помощью “рычага” Жуковского.

К повёрнутому на 900 плану скоростей в одноимённые точки приложим все силы, действующие на механизм, в том числе и силы инерции. Составим уравнение моментов всех сил относительно полюса плана скоростей с учётом знаков и определим уравновешивающую силу.

Определим расхождение результатов расчёта уравновешивающего момента, полученных выше использованными методами.

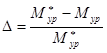(2.25)

Полученная погрешность составляет 1%, что меньше предельно допускаемого значения в 5%.

3.Синтез кинематической схемы планетарного редуктора и построение картины эвольвентного зацепления

3.1 Задание

3.1.1 Модуль зубчатых колёс планетарного механизма: m1= 3 мм

Числа зубьев колёс простой передачи: Z1=15 , Z2=30;

Модуль зубчатых колёс Z1и Z2: m=6 мм;

Все зубчатые колёса должны быть нулевыми. А это значить, что во избежание подреза ножки зуба для колёс с внешним зацеплением принимают Z>17, для колёс с внутренним зацеплением Z>85.

Подберём числа зубьев Z1,Z2,Z3 для зубчатой передачи с передаточным отношением U=nдв/n1=720/62=11,6.

Задаёмся числом зубьев Z1 из ряда Z1=17,18,19,…. Пусть Z1=20. Число зубьев Z3 найдём из выражения:

(3.1)