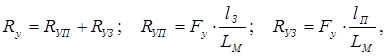Курсовая работа: Расчёт на прочность кузова автомобиля ВАЗ 2108
Геометрия конструкции моделируется совокупностью элементов различной размерности и различных форм, представляющих три группы:
одномерные элементы, имеющие форму прямой линии или дуги окружности;
двумерные элементы треугольной и четырехугольной формы;
трехмерные элементы - тетраэдры, гексаэдры и пятигранники.
При моделировании требуемых упруго-массовых свойств конструкции кроме геометрии конечных элементов учитываются их свойства, то есть способность воспринимать нагрузку и испытывать деформацию определенного вида. Так, например, некоторая часть одномерных элементов конструкции может работать только на растяжение-сжатие, а другая может к тому же воспринимать изгиб и кручение.
Для моделирования граничных условий и массовых свойств конструкции предназначены специальные элементы, образующие группу «другие» (other).
Расположение элемента в пространстве зависит от координат узлов, принадлежащих элементу. В узлах определяются обобщенные узловые смещения. Узловыми смещениями могут быть компоненты вектора перемещений вдоль осей координат и углы поворота элемента в узлах вокруг осей координат. Обобщенные узловые смещения обозначаются термином степени свободы или сокращенно DOF (degreesoffreedom).
Набор или список степеней свободы модели зависит от типа элементов, используемых при моделировании.
Так, в узлах элементов работающих на изгиб и кручение (элементы балки и оболочки) определены все шесть компонентов смещений, а в узлах трехмерных элементов - только перемещения вдоль осей координат. Если в модели нет элементов, работающих на изгиб, то список степеней свобод не будет содержать углы поворота элементов в узлах. Это не означает, что их нет, просто углы поворота не оказывают влияние на величину полной потенциальной энергии конструкции.
1.2 Нагрузочные режимы
В процессе эксплуатации на КМ действуют нагрузки, возникающие при ее движении по дорожной поверхности, которые обычно носят случайный характер. Их можно подразделить на случайные и детерминированные. Эти нагрузки действуют на несущую систему КМ и образуют пространственную систему. Определение величин и направлений нагрузок - достаточно сложная задача, поэтому при расчетах из всей совокупности учитывают нагрузки, которые возникают в экстремальных условиях эксплуатации (предельные нагрузки) (рис. 1.2.1).
Рассмотрим экстремальные детерминированные нагрузки и соответствующие им режимы эксплуатации. Статические расчеты несущих систем КМ выполняют для симметричных (изгиб), кососимметричных (кручение) и боковых (в горизонтальной плоскости) нагрузок.
Вертикальную симметричную нагрузку RZ (рис. 1.2.1, а) можно вычислить, используя выражение

где GHj - вес i-го неподрессоренного узла или агрегата КМ, kД -коэффициент динамичности, принимаемый в зависимости от типа КМ: для грузовых
kД = 3,0; для КМ высокой проходимости kД = 3,5...4,0; для легковых КМ и автобусов kД =2,0...2,5; п - число колес, взаимодействующих с опорной поверхностью.
Вертикальная несимметричная нагрузка возникает при наезде колесом на препятствие и при вывешивании колеса (или колес) (рис. 1.2.1, б). В первом случае вертикальную несимметричную нагрузку можно определить по приведенной выше формуле, учитывая, что kД = 1,5 для грузовых КМ;
kД = 1,8 для автомобилей высокой проходимости; kД = 1,3 для легковых КМ и автобусов.

Рис. 1.2.1. Расчетные режимы нагружения: а - вертикальная симметричная нагрузка; б - наезд колесом на препятствие и вывешивание колеса; в - горизонтальная нагрузка при движении по криволинейной траектории; г - наезд колесом на ступенчатое препятствие; д - движение КМ по воде
Момент, закручивающий несущую систему, равен
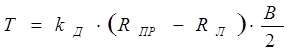
Здесь RПР , RЛ - нагрузки на правом (R1 ) и левом (R2 ) передних колесах соответственно, В - колея.
При расчете несущей системы на изгиб от действия вертикальных нагрузок необходимо учитывать координаты точек их приложения. Динамические нагрузки в этом случае характеризуются эмпирическими коэффициентами (например, коэффициентом динамичности).
Боковые силы действуют на КМ при ее движении по криволинейной траектории (рис. 1.2.1, в), в случае появления несимметричных нагрузок при тяговом и тормозном режимах, а также при боковом столкновении с препятствием.
Максимально возможная центробежная сила Fyдо переворота при криволинейном движении определяется следующим выражением (см. рис. 1.2.1. в)
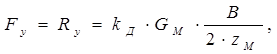
где Ry – реакция от дороги на колёса, zM – расстояние от опорной поверхности до центра масс КМ. При этом