Курсовая работа: Расчет передаваемой части телемеханики

Рисунок 1.5 – График спектральной плотности мощности
S(ω)= 2*√π/√ α*exp(-ω2/4α2)
1.2.3 Расчет верхней частоты аналитическим методом
Аналогично 1.1.3 с помощью теоремы Парсеваля:
 | (1.9) |
 | (1.10) |
 | (1.11) |
 | (1.12) |
| (1.13) |
В левой части мы имеем функцию Лапласа. Значению Ф(z) = 0.48 соответствует значение z=2.03. Следовательно
ωв = 0,03 * 2,03 = 0,0609 рад/с
1.2.4 Расчет верхней частоты графическим методом
Аналогично 1.1.4
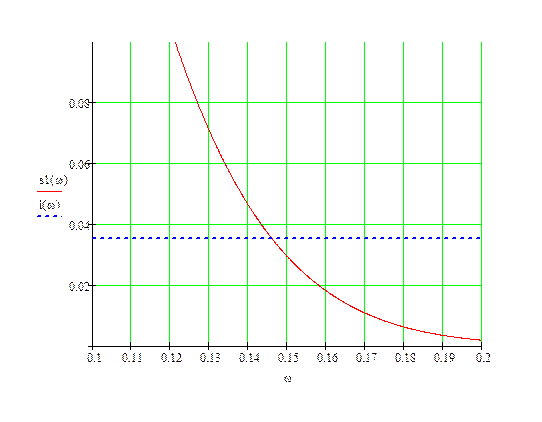
Рисунок 1.6 – Определение верхней частоты
Определяем значение верхней частоты:
![]() рад/с
рад/с
1.3 Определение периода опроса
Период опроса определяется согласно теореме Котельникова: для передачи непрерывной функции времени со спектром ограниченным некоторой верхней частотой f в , достаточно передавать её отдельные значения через промежуток:
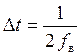 | (1.14) |
Это выражение применимо только в идеальном случае, когда известны все значения функции на бесконечном интервале времени. Поскольку это невозможно, временные промежутки принимаются меньшими:
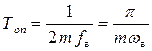 | (1.15) |
Коэффициент m в данной работе принимается равным 3.
Среди полученных значений верхней частоты выбираем наибольшее, т.е. ![]() рад/с и используя формулу (1.15) найдем период опроса:
рад/с и используя формулу (1.15) найдем период опроса:
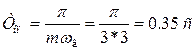
2 Определение полосы занимаемых частот
2.1 Временное разделение каналов
При временном разделении каналов вначале в линию связи посылается сигнал начала цикла τинц , потом передается информация первого канала τии , потом импульс синхронизации τси , который переключает распределители на второй канал, а далее все повторяется. Каждый импульс передается спустя паузу τп (рис. 2.1).
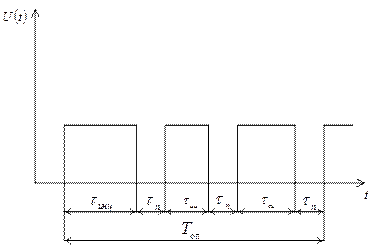
Рисунок 2.1 – Диаграмма временного разделения каналов
Получаем, что
| (2.1) |
где k – количество разрядов кода.
Учитывая, что τинц =2τ, τп =τии =τ, τси =1,5τ, получаем
| (2.2) | |
Таким образом, период импульсной последовательности равен ![]() с.
с.
Определим количество разрядов кода из условий:
| (2.3) | |
| (2.4) |
где δ’ – допустимая погрешность передачи, а D– динамический диапазон, т.е. отношение наибольшего (из возможных) уровня сигнала к наименьшему.
Решая неравенства получаем
Значит
k=6
Зная, что практическая ширина спектра ограничена пятой гармоникой, получаем, что диапазон частот по обе стороны от несущей:
| (2.5) |
где
| (2.6) | |
Следовательно, полоса частот, занимаемая каналом, будет равна
| (2.7) |
Построим спектральную диаграмму, учитывая, что при кодовой манипуляции каждый разряд кода передается во времени на своей частоте.
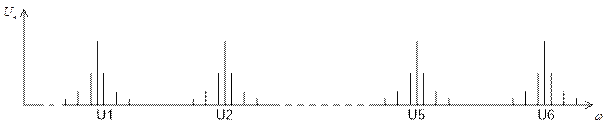
Рисунок 2.2 – Спектр сигнала при временном разделении
2.2 Частотное разделение каналов