Курсовая работа: Расчет высоковольтного генератора импульсных напряжений

Расстояние от шаров до корпусов и вводов конденсаторов должно составлять:

м.

3.5 Определение собственной индуктивности ГИН

Индуктивность катушки определяется как ,

где – сечение катушки, – число витков тока ( – числу ступеней ГИН),

длина ГИН: м.

,

где – расстояние между клеммами, – высота конденсатора до клемм: м, м;

м² .

Индуктивность катушки:

Гн.

Суммарная индуктивность конденсаторов:

Гн.

Собственная индуктивность ГИН:

Гн.

3.6 Определение индуктивности внешнего контура ГИН.

Длина внешнего контура равна: ,

где – высота ГИН до клемм конденсаторов,

высота конденсатора до клемм: м,

длина шины подключения нагрузки: м,

длина ГИН: м.

Опорные изоляторы выбираются так, чтобы их полная высота составляла: , при кВ/мм высота опорных изоляторов: м.

Таким образом из таблицы 2, в соответствии с приведенной выше формулой, выбираем четыре опорных изолятора типа 3×ОНС–10–500, высота которых в сумме равна м.

Рассчитаем длину внешнего контура:

,

м.

Определяем индуктивность прямолинейных участков проводов по формуле:

Гн.

Выполнив необходимые расчеты, можно определить полную индуктивность разрядного контура ГИН:

Гн.

4. Расчет переходных процессов в разрядной цепи ГИН.

На рис.1 приведен контур цепи разряда ГИН.

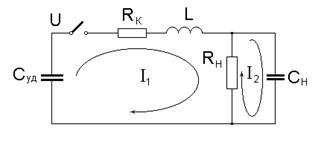
Рис. 1.

Напряжение на нагрузке: , где .

Для перехода к оригиналу необходимо произвести преобразования для приведения изображения к табличному виду, имеющему оригинал:

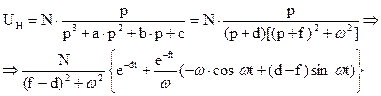
Рассчитаем коэффициенты операторного уравнения – (1), при .

,

,

.

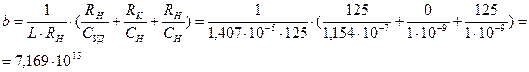Для дальнейшего расчета применим формулу Кардано. В уравнении введем новую переменную:. После подстановки уравнение примет вид:

, где: ; ,

,

.

Уравнение (1) имеет один действительный корень и два сопряженных комплексных корня.

Действительный корень:

, где ,

.

Комплексные корни: ,

, .