Курсовая работа: Разработка эквивалентных и принципиальных схем электрического фильтра и усилителя напряжения

- - амплитуда при синусах;

- - амплитуда при косинусах;

- , φ=arctg() - амплитуда и фаза произвольной гармоники входного сигнала;

- - номер гармоник;

- - частоты гармоник.

У чётных сигналов , а у нечётных . Кроме того может отсутствовать постоянная составляющая в сигнале.

При определении коэффициентов ряда Фурье функцию под знаком интеграла для чётных и нечётных функций можно задавать на части периода, а результат вычислений округлять в большую сторону.

4.2 Анализ спектра

Для сигнала на рисунке 9:

;

-для периода от 0 до T/4.

Функция в данном варианте чётная (т. е. ), содержит постоянную составляющую. Определяем :

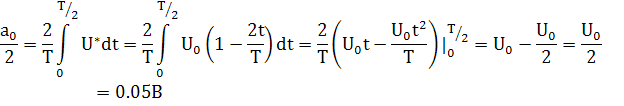
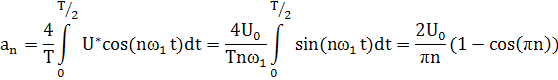
Таким образом, в спектре сигнала нет чётных гармоник; но по четным порядкам сигнал равен нулю

С учётом этого, аналитическое выражении сигнала для сигнала на входе фильтра:

U(t)_вхФ =a₁ cos(w₁ t)+a₃ cos(3w₁ t)+a₅ cos(5w₁ t)+b₇ cos(7w₁ t)+…=0,127 cos(w₁ t)+0,042 cos(w₁ t)+ 0,025 cos(5w₁ t) + 0.018 cos(7w₁ t)+ 0.014 cos(9w₁ t)+… .

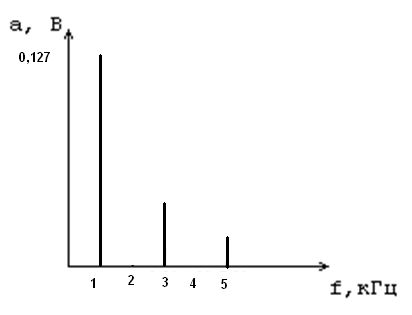Рисунок 12 – График амплитудного спектра сигнала

5 Анализ прохождения входного сигнала через радиотехническое устройство