Курсовая работа: Разработка приложений в визуальной среде Delphi на языке программирования Object Pascal
Для стороны b: a2=y3-y2; b2=x2-x3; c2= (-x2) ∙ (y3-y2) +y2∙ (x3-x2).
Для стороны c: a3=y1-y3; b1=x3-x1; c3= (-x3) ∙ (y1-y3) +y3∙ (x1-x3).
Расстояние от точки, заданной координатами (х4 , у4 ), до сторон треугольника a, b, c может быть определено по формуле (1.5):
d1 =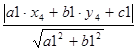 ;
;
d2 =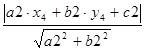 ;
;
d3 =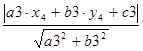 .
.
Определим систему ограничений для решения данной задачи. Если рассмотреть на формулу (1.5) нахождения расстояния от точки, заданной координатами (х4 , у4 ), до прямой, заданной уравнением (1.1), то необходимым и достаточным условием существования выражения является неравенство [2]:
![]() ≠ 0. (1.6)
≠ 0. (1.6)
Таким образом, применяя формулу (1.6) для решения задачи запишем систему ограничений:
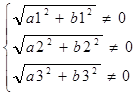 . (1.7)
. (1.7)
По условию задачи исходными данными являются координаты вершин треугольника, поэтому систему ограничений для данной задачи дополним условием существования треугольника:
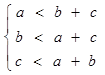 . (1.8)
. (1.8)
Определим длины сторон треугольника по формуле расстояния между двумя точками [2]:
d=![]() . (1.9)
. (1.9)
Для треугольника со сторонами a,b,c формула (1.9) имеет вид:
a=![]() ,
,
b=![]() ,
,
c=![]() .
.
Вычисленные длины сторон треугольника применим к системе ограничений (1.8). Таким образом, в задаче рассматривается две системы ограничений (1.7), (1.8) для необходимого и достаточного условия существования решения.
1.2 Задача 2. Математическая модель
Во второй задаче по теоретической механике необходимо создать приложение, которое будет отображать визуальное перемещение объектов в соответствии с кинематической схемой, рисунок 1 (Кинематическая схема).
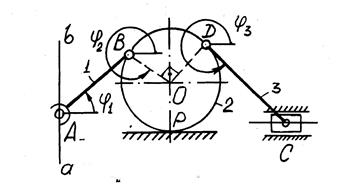
Рисунок 1 - Кинематическая схема
На данном механизме (рисунок 1 (Кинематическая схема)) имеется одна неподвижная опора, на которой находится подвижный барабан, к нему на шарнирах прикреплены стержни [5]. Один стержень связан шарниром с ползуном и движется вдоль горизонтальной направляющей [5]. Другой стержень шарниром соединен с неподвижной осью и движется в вертикальном направлении [5].
В качестве переменной, определяющей положение, механизма задана переменная W. В таком случае положение механизма однозначно определяется переменной W. В зависимости от изменения положения вращающегося звена изменяется положение механизма в целом. Вращающееся звено может изменять положение в первой четверти декартовой системы координат. Зададим точки, определяющие положение механизма, рисунок 2 (Точки, определяющие положение механизма).
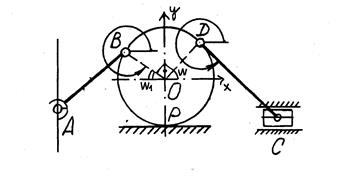
Рисунок 2 - Точки, определяющие положение механизма
На основании схемы приведенной на рисунке 2 (Точки, определяющие положение механизма), составим математическую модель, описывающую положение механизма в зависимости от изменения угла W. В связи с изменением геометрических параметров механизма на плоскости, принимаем за текущую декартову систему координат с направлением осей X и Y.
Радиус окружности барабана задает сам пользователь в форме, причем OD = OB = R. Координаты точки О (х0, у0) задаются в программе. Размер стержней принимается за постоянную величину и определяется пользователем. Угол W задается пользователем в форме. Изменяя значение угла W, будет изменяться положение механизма.
Определим координаты точки D.