Курсовая работа: Разработка программного обеспечения для нахождения корней биквадратного уравнения
Ответ: ![]() .
.
Пример 2.
Решить биквадратное уравнение.
2х4 – 5х2 +2=0
Решение:
Обозначим х2 =t. Тогда х4 =(х2 )2 =t2 и уравнение примет вид:
2t2 –5t+2=0
D=(–5)2 – 4(2)(2)=25 – 16 = 9 > 0,
t1 =(5+3) / 4=2 и t2 =(5 – 3) / 4=1 / 2.
Так как t=x2 , то корни исходного уравнения найдем в результате решения уравнений
х1 =2 и х2 =1/2.
Имеем 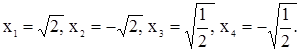
Ответ: 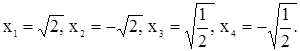
2. Математические и алгоритмические основы решения задачи
Рассмотрим биквадратное уравнение
ax4 + bx2 + c = 0.
Введем подстановку
y = x2 .
Получим квадратное уравнение общего вида
ay2 + by + c = 0.
Таким образом, для решения биквадратного уравнения необходимо помнить, что оно свелось к системе двух уравнений второй степени:
y = x2
ay2 + by + c = 0.
Решим квадратное уравнение относительно переменной "y". Получим три возможных варианта решений:
дискриминант отрицателен: уравнение не имеет действительных решений;
дискриминант не отрицателен и равен нулю: уравнение имеет один двукратный корень;
дискриминант не отрицателен и равен нулю: уравнение имеет два различных корня.
В первом случае, когда дискриминант квадратного уравнения отрицателен, система не имеет решения, так как одно из входящих в нее уравнений, а именно квадратное уравнение ay2 + by + c = 0, не имеет решения.
Последние два случая соответствуют неотрицательному дискриминанту квадратного уравнения. Квадратное уравнение имеет действительные решения. Однако, обратите внимание на тот факт, что первое уравнение системы ax2 = y имеет смысл только при значениях y>=0. Поэтому, если оба корня квадратного уравнения ay2 +by +c = 0 отрицательны, система уравнений так же не имеет решения. Кроме того, если хотя бы один из корней квадратного уравнения ay2 +by +c = 0 отрицательный, система уравнений будет иметь только два действительных решения.
И только в том случае, когда оба корня квадратного уравнения неотрицательны, система уравнений имеет четыре действительных решения. Дадим теперь словесное описание алгоритма.