Курсовая работа: Разработка программы нахождения всех полных подграфов (клик) данного графа

Стратегия тестирования

Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы.

1. Тестирование на пустом графе.

Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) клик в нем нет.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Рисунок 3.5. Сообщение об отсутствии клик в графе.

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

2. Тестирование на графе с единственной вершиной.

Теоретические расчеты: граф не содержит клик - подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

3.Тестирование на графе с тремя не соединенными ребрами вершинами.

Теоретические расчеты: аналогичны расчетом в пункте 2.

Практический результат: клик в графе не найдено, получено соответствующее уведомление (рисунок 3.5).

Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

4.Тестирование на графе из двух вершин, соединенных ребром.

Теоретические расчеты: граф удовлетворяет понятию "клика".

Практические результаты: найдена одна клика, представляющая собой данный граф.Результат: теоретические и практические расчеты сходятся – на данном наборе алгоритм работает верно.

Тестирование на сложном графе.

В программе был создан граф, представленный на рисунке 3.6.

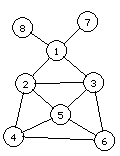
Рисунок 3.6. Сложный граф, используемый в тесте.

Матрица смежности графа:

100011

10111000

11001100

01001100

01110100