Курсовая работа: Разработка программы решения системы линейных уравнений

А=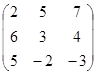

∆=-1, значит, существует обратная матрица .

Матрица - столбец при неизвестных:

Х =

Матрица - столбец из свободных членов:

В =

Тогда решение запишется в виде

==

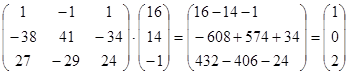
Откуда следует, х₁ = 1; х₂ = 0; х₃ = 2.

1.3 Вычисление определителей второго и третьего порядка

Число (а ₁₁ а ₂₂ - а ₁₂ а ₂₁ ) называется определителем второго порядка и обозначается символом

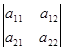
Определитель второго порядка содержит две строки и два столбца. Числа а ₁₁ , а ₁₂ , а ₂₁ , а ₂₂ называются элементами определителя. Диагональ определителя, на которой расположены числа а ₁₁ , а ₂₂ - главная, а элементы а ₁₂ , а ₂₁ составляют побочную диагональ.

Определитель 3-го порядка содержит три строки и три столбца:

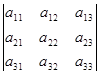
Для вычисления определителя третьего порядка существует несколько способов.

Рассмотрим метод вычисления определителя разложением по элементам первой строки.

Введем понятие минора и алгебраического дополнения.

Минором некоторого элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца в которых этот элемент расположен. Обозначается М_{ij (} i - номер строки, j - номер столбца).

Например, минором элемента а₁₂ является определитель

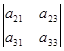
Алгебраическим дополнением данного элемента определителя называется его минор, умноженный на (-1) ^{i+ j} . Алгебраические дополнения обозначаются буквами А_ij, и тогда А_y = (-1) ^{i+ j} M_y .

Определитель вычисляется так:

=.

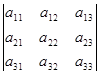Так же можно разложить определитель по любой строке или столбцу.

Изложенный метод применим к вычислению определителей 4-го и т.д. порядков.

Пример3. Вычислить определитель разложением по элементам первой строки

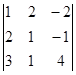
Решение: Элементы первой строки